Przykładami są własności logarytmów o różnych podstawach. Równania logarytmiczne o różnych podstawach. Podstawowe własności logarytmu

Logarytmy, podobnie jak wszystkie liczby, można dodawać, odejmować i przekształcać w dowolny sposób. Ale ponieważ logarytmy nie są zwykłymi liczbami, istnieją tutaj reguły, które nazywają się podstawowe właściwości.

Znajomość tych zasad jest konieczna – bez nich nie można rozwiązać żadnego poważnego problemu logarytmicznego. W dodatku jest ich bardzo mało – wszystkiego można się nauczyć w jeden dzień. Więc zacznijmy.

Dodawanie i odejmowanie logarytmów

Rozważ dwa logarytmy o tej samej podstawie: log a x i loguj a tak... Następnie można je dodawać i odejmować oraz:

1. Dziennik a x+ log a tak= log a (x · tak);
2. Dziennik a x- Dziennik a tak= log a (x : tak).

Zatem suma logarytmów jest równa logarytmowi iloczynu, a różnica jest logarytmem ilorazu. Pamiętaj, że kluczową kwestią jest tutaj: identyczne podstawy... Jeśli powody są różne, te zasady nie działają!

Te formuły pomogą ci obliczyć wyrażenie logarytmiczne, nawet jeśli niektóre jego części nie są liczone (zobacz lekcję „Co to jest logarytm”). Spójrz na przykłady - i zobacz:

Dziennik 6 4 + dziennik 6 9.

Ponieważ podstawy logarytmów są takie same, używamy wzoru sumy:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Zadanie. Znajdź wartość wyrażenia: log 2 48 - log 2 3.

Bazy są takie same, stosujemy wzór różnicy:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Zadanie. Znajdź wartość wyrażenia: log 3 135 - log 3 5.

Znowu podstawy są takie same, więc mamy:
log 3 135 - log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Jak widać, oryginalne wyrażenia składają się ze „złych” logarytmów, które nie są oddzielnie liczone. Ale po przekształceniach otrzymuje się całkiem normalne liczby. Wiele testów opiera się na tym fakcie. Ale jaka kontrola - takie wyrażenia z całą powagą (czasami - praktycznie niezmienione) są oferowane na egzaminie.

Usunięcie wykładnika z logarytmu

Teraz trochę skomplikujmy zadanie. Co się stanie, jeśli podstawa lub argument logarytmu opiera się na stopniu? Następnie wykładnik tego stopnia można wyciągnąć ze znaku logarytmu według następujących zasad:

Łatwo zauważyć, że ostatnia zasada jest zgodna z dwoma pierwszymi. Ale lepiej o tym pamiętać - w niektórych przypadkach znacznie zmniejszy to ilość obliczeń.

Oczywiście wszystkie te reguły mają sens przy obserwacji ODZ logarytmu: a > 0, a ≠ 1, x> 0. I jeszcze jedno: naucz się stosować wszystkie formuły nie tylko od lewej do prawej, ale także na odwrót, tj. możesz wpisać liczby przed znakiem logarytmu do samego logarytmu. To jest najczęściej wymagane.

Zadanie. Znajdź wartość wyrażenia: log 7 49 6.

Pozbądźmy się stopnia w argumencie za pomocą pierwszej formuły:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Zadanie. Znajdź znaczenie wyrażenia:

[Podpis pod rysunkiem]

Zauważ, że mianownik zawiera logarytm, którego podstawą i argumentem są dokładne potęgi: 16 = 2 4; 49 = 7 2. Mamy:

[Podpis pod rysunkiem]

Myślę, że ostatni przykład wymaga wyjaśnienia. Gdzie zniknęły logarytmy? Do ostatniej chwili pracujemy tylko z mianownikiem. Przedstawiliśmy podstawę i argument stojącego tam logarytmu w postaci stopni i wydobyliśmy wskaźniki - otrzymaliśmy ułamek „trzypiętrowy”.

Spójrzmy teraz na ułamek podstawowy. Licznik i mianownik zawierają tę samą liczbę: log 2 7. Ponieważ log 2 7 ≠ 0 możemy skreślić ułamek - mianownik pozostaje 2/4. Zgodnie z zasadami arytmetyki czwórkę można przenieść do licznika, co zostało zrobione. Rezultatem była odpowiedź: 2.

Przeprowadzka do nowej fundacji

Mówiąc o zasadach dodawania i odejmowania logarytmów, szczególnie podkreśliłem, że działają one tylko dla tych samych podstaw. A jeśli powody są inne? A co, jeśli nie są to dokładne potęgi o tej samej liczbie?

Na ratunek przychodzą formuły przejścia na nowy fundament. Sformułujmy je w postaci twierdzenia:

Niech logarytm logarytmuje a x... Następnie dla dowolnej liczby C takie, że C> 0 i C≠ 1, równość jest prawdziwa:

[Podpis pod rysunkiem]

W szczególności, jeśli umieścimy C = x otrzymujemy:

[Podpis pod rysunkiem]

Z drugiej formuły wynika, że ​​można zamienić podstawę i argument logarytmu, ale w tym przypadku całe wyrażenie jest „odwrócone”, tj. logarytm pojawia się w mianowniku.

Te formuły rzadko występują w konwencjonalnych wyrażeniach liczbowych. Można oszacować, jak wygodne są one tylko przy rozwiązywaniu równań logarytmicznych i nierówności.

Istnieją jednak zadania, które zazwyczaj nie są rozwiązywane z wyjątkiem przejścia do nowej fundacji. Rozważ kilka z nich:

Zadanie. Znajdź wartość wyrażenia: log 5 16 log 2 25.

Zauważ, że argumenty obu logarytmów zawierają dokładne stopnie. Wyjmijmy wskaźniki: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Teraz „odwróćmy” drugi logarytm:

[Podpis pod rysunkiem]

Ponieważ iloczyn nie zmienia się z permutacji czynników, spokojnie pomnożyliśmy cztery i dwa, a następnie zajęliśmy się logarytmami.

Zadanie. Znajdź wartość wyrażenia: log 9 100 · lg 3.

Podstawą i argumentem pierwszego logarytmu są dokładne stopnie. Zapiszmy to i pozbądźmy się metryk:

[Podpis pod rysunkiem]

Pozbądźmy się teraz logarytmu dziesiętnego, przechodząc do nowej podstawy:

[Podpis pod rysunkiem]

Podstawowa tożsamość logarytmiczna

Często w procesie rozwiązywania wymagane jest przedstawienie liczby jako logarytmu do danej podstawy. W takim przypadku pomogą nam formuły:

W pierwszym przypadku liczba n staje się wskaźnikiem stopnia stojącego w sporze. Numer n może być absolutnie wszystkim, ponieważ jest to tylko wartość logarytmu.

Druga formuła jest właściwie sparafrazowaną definicją. Nazywa się to: podstawową tożsamością logarytmiczną.

Rzeczywiście, co się stanie, jeśli liczba b do takiej potęgi, że liczba b do tego stopnia daje liczbę a? Zgadza się: otrzymujesz ten sam numer a... Przeczytaj uważnie ten akapit jeszcze raz - wiele osób "wisi" na nim.

Podobnie jak formuły przejścia do nowej bazy, podstawowa tożsamość logarytmiczna jest czasami jedynym możliwym rozwiązaniem.

Zadanie. Znajdź znaczenie wyrażenia:

[Podpis pod rysunkiem]

Zauważ, że log 25 64 = log 5 8 - po prostu przesunąłeś kwadrat z podstawy i argumentu logarytmu. Biorąc pod uwagę zasady mnożenia stopni o tej samej podstawie, otrzymujemy:

[Podpis pod rysunkiem]

Jeśli ktoś nie wie, to był prawdziwy problem z egzaminu :)

Jednostka logarytmiczna i zero logarytmiczne

Na zakończenie podam dwie tożsamości, które trudno nazwać własnościami – są to raczej konsekwencje definicji logarytmu. Nieustannie napotykają na problemy i, co zaskakujące, stwarzają problemy nawet „zaawansowanym” studentom.

1. Dziennik a a= 1 to jednostka logarytmiczna. Pamiętaj raz na zawsze: logarytm do dowolnej podstawy a od tej samej podstawy równa się jeden.
2. Dziennik a 1 = 0 to zero logarytmiczne. Baza a może być cokolwiek, ale jeśli argument jest jeden, logarytm wynosi zero! ponieważ a 0 = 1 jest bezpośrednią konsekwencją definicji.

To wszystkie właściwości. Pamiętaj, aby przećwiczyć wprowadzanie ich w życie! Pobierz ściągawkę na początku lekcji, wydrukuj ją i rozwiąż problemy.

Instrukcje

Zapisz podane wyrażenie logarytmiczne. Jeśli wyrażenie używa logarytmu 10, to jego zapis jest obcinany i wygląda tak: lg b jest logarytmem dziesiętnym. Jeśli logarytm ma za podstawę liczbę e, to zapisz wyrażenie: ln b - logarytm naturalny. Zrozumiałe jest, że wynikiem dowolnego jest potęga, do której liczba podstawowa musi zostać podniesiona, aby uzyskać liczbę b.

Znajdując sumę dwóch funkcji, wystarczy je kolejno rozróżnić i dodać wyniki: (u + v) "= u" + v ";

Znajdując pochodną iloczynu dwóch funkcji, należy pomnożyć pochodną pierwszej funkcji przez drugą i dodać pochodną drugiej funkcji pomnożoną przez pierwszą funkcję: (u * v) "= u" * v + v "* u;

Aby znaleźć pochodną ilorazu dwóch funkcji, należy od iloczynu pochodnej dywidendy pomnożonej przez funkcję dzielnika odjąć iloczyn pochodnej dzielnika pomnożony przez funkcję dywidendy, i podziel to wszystko przez kwadrat funkcji dzielnika. (u / v) "= (u" * v-v "* u) / v^ 2;

Jeżeli dana jest funkcja zespolona, ​​to należy pomnożyć pochodną funkcji wewnętrznej i pochodną funkcji zewnętrznej. Niech y = u (v (x)), a następnie y "(x) = y" (u) * v "(x).

Korzystając z tych uzyskanych powyżej, możesz rozróżnić prawie każdą funkcję. Spójrzmy więc na kilka przykładów:

y = x ^ 4, y "= 4 * x ^ (4-1) = 4 * x ^ 3;

y = 2 * x ^ 3 * (e ^ xx ^ 2 + 6), y "= 2 * (3 * x ^ 2 * (e ^ xx ^ 2 + 6) + x ^ 3 * (e ^ x-2 * x));
Istnieją również problemy z obliczaniem pochodnej w punkcie. Niech zostanie podana funkcja y = e ^ (x ^ 2 + 6x + 5), musisz znaleźć wartość funkcji w punkcie x = 1.
1) Znajdź pochodną funkcji: y "= e ^ (x ^ 2-6x + 5) * (2 * x +6).

2) Oblicz wartość funkcji w danym punkcie y "(1) = 8 * e ^ 0 = 8

Powiązane wideo

Pomocna rada

Poznaj tabelę pochodnych elementarnych. To znacznie zaoszczędzi czas.

Źródła:

• pochodna stałej

Jaka jest więc różnica między równaniem irracjonalnym a racjonalnym? Jeśli nieznana zmienna znajduje się pod pierwiastkiem kwadratowym, równanie jest uważane za irracjonalne.

Instrukcje

Główną metodą rozwiązywania takich równań jest metoda konstruowania obu części równania w kwadracie. Jednakże. to naturalne, pierwszym krokiem jest pozbycie się znaku. Ta metoda nie jest trudna technicznie, ale czasami może wpędzić Cię w kłopoty. Na przykład równanie v (2x-5) = v (4x-7). Dodając obie strony do kwadratu, otrzymujesz 2x-5 = 4x-7. To równanie nie jest trudne do rozwiązania; x = 1. Ale liczba 1 nie będzie podana równania... Czemu? Podstaw 1 w równaniu dla x, a zarówno prawa, jak i lewa strona będą zawierały wyrażenia, które nie mają sensu. Ta wartość nie jest prawidłowa dla pierwiastka kwadratowego. Dlatego 1 jest pierwiastkiem obcym, a zatem dane równanie nie ma pierwiastków.

Tak więc irracjonalne równanie jest rozwiązywane za pomocą metody podniesienia do kwadratu obu jego stron. A po rozwiązaniu równania konieczne jest odcięcie obcych korzeni. Aby to zrobić, zastąp znalezione korzenie oryginalne równanie.

Rozważ inny.
2x + vx-3 = 0
Oczywiście to równanie można rozwiązać w taki sam sposób, jak poprzednie. Przenieś kompozyt równania które nie mają pierwiastka kwadratowego, po prawej stronie, a następnie użyj metody do kwadratu. rozwiązać powstałe równanie racjonalne i pierwiastki. Ale też inny, bardziej pełen wdzięku. Wprowadź nową zmienną; vx = y. W związku z tym otrzymujesz równanie postaci 2y2 + y-3 = 0. To znaczy zwykłe równanie kwadratowe. Znajdź jego korzenie; y1 = 1 i y2 = -3 / 2. Następnie zdecyduj dwa równania vx = 1; vx = -3 / 2. Drugie równanie nie ma pierwiastków, z pierwszego dowiadujemy się, że x = 1. Nie zapomnij sprawdzić korzeni.

Rozwiązywanie tożsamości jest dość łatwe. Wymaga to wykonania identycznych przekształceń, aż do osiągnięcia celu. W ten sposób za pomocą najprostszych operacji arytmetycznych zadanie zostanie rozwiązane.

Będziesz potrzebować

• - papier;
• - długopis.

Instrukcje

Najprostszym z takich przekształceń jest skrócone mnożenie algebraiczne (np. kwadrat sumy (różnica), różnica kwadratów, suma (różnica), sześcian sumy (różnica)). Ponadto istnieje wiele wzorów trygonometrycznych, które są zasadniczo tymi samymi tożsamościami.

Rzeczywiście, kwadrat sumy dwóch wyrazów jest równy kwadratowi pierwszego plus dwukrotność iloczynu pierwszego przez drugi i plus kwadrat drugiego, czyli (a + b) ^ 2 = (a + b) (a + b) = a ^ 2 + ab + ba + b ^ 2 = a ^ 2 + 2ab + b ^ 2.

Uprość oba

Ogólne zasady rozwiązania

Przejrzyj podręcznik rachunku różniczkowego lub wyższej matematyki, która jest całką oznaczoną. Jak wiecie, rozwiązanie całki oznaczonej jest funkcją, której pochodna da całkę. Ta funkcja nazywa się funkcją pierwotną. Zgodnie z tą zasadą konstruowane są całki podstawowe.
Określ formę całki, która z całek tabelarycznych jest odpowiednia w tym przypadku. Nie zawsze da się to od razu ustalić. Często widok tabelaryczny staje się zauważalny dopiero po kilku przekształceniach w celu uproszczenia całki.

Zmienna metoda zastępowania

Jeśli całka jest funkcją trygonometryczną, w argumencie której występuje jakiś wielomian, spróbuj użyć metody zmiany zmiennej. Aby to zrobić, zastąp wielomian w argumencie całki jakąś nową zmienną. Określ nowe granice integracji na podstawie relacji między nową i starą zmienną. Rozróżniając to wyrażenie, znajdź nową różnicę w. W ten sposób otrzymasz nową formę poprzedniej całki, zbliżoną lub nawet odpowiadającą jakiejś tabelarycznej.

Rozwiązanie całek drugiego rodzaju

Jeśli całka jest całką drugiego rodzaju, wektorową postacią całki, to będziesz musiał zastosować reguły przejścia od tych całek do skalarnych. Jedną z tych zasad jest stosunek Ostrogradskiego do Gaussa. To prawo umożliwia przejście od strumienia wirnika określonej funkcji wektorowej do całki potrójnej po rozbieżności danego pola wektorowego.

Zastąpienie granic integracji

Po znalezieniu funkcji pierwotnej konieczne jest zastąpienie granic integracji. Najpierw wstaw górną wartość graniczną do wyrażenia pierwotnego. Dostaniesz numer. Następnie odejmij od otrzymanej liczby inną liczbę uzyskaną z dolnej granicy do funkcji pierwotnej. Jeśli jedną z granic całkowania jest nieskończoność, to przy podstawieniu jej w funkcję pierwotną należy przejść do granicy i znaleźć to, do czego dąży wyrażenie.
Jeśli całka jest dwuwymiarowa lub trójwymiarowa, będziesz musiał zobrazować geometrycznie granice całkowania, aby zrozumieć, jak obliczyć całkę. Rzeczywiście, w przypadku, powiedzmy, trójwymiarowej całki, granicami całkowania mogą być całe płaszczyzny, które ograniczają całkowaną objętość.

Wynika z jego definicji. A więc logarytm liczby b z powodu a jest definiowany jako wskaźnik stopnia, w jakim liczba musi zostać podniesiona a zdobyć numer b(Logarytm istnieje tylko dla liczb dodatnich).

Z tego sformułowania wynika, że ​​obliczenia x = log a b, jest równoważne rozwiązaniu równania a x = b. Na przykład, log 2 8 = 3 ponieważ 8 = 2 3 ... Sformułowanie logarytmu pozwala wykazać, że jeśli b = a c, to logarytm liczby b z powodu a jest równe z... Jasne jest również, że temat logarytmowania jest ściśle powiązany z tematem potęgi liczby.

Z logarytmami, jak z dowolnymi liczbami, możesz to zrobić operacje dodawania, odejmowania i przekształcać się w każdy możliwy sposób. Ale ze względu na to, że logarytmy nie są zwykłymi liczbami, obowiązują tutaj specjalne zasady, które nazywają się podstawowe właściwości.

Dodawanie i odejmowanie logarytmów.

Weźmy dwa logarytmy o tych samych podstawach: zarejestruj x oraz zaloguj się... Następnie usuń możliwe jest wykonywanie operacji dodawania i odejmowania:

log a x + log a y = log a (x y);

log a x - log a y = log a (x: y).

zaloguj się(x 1 . x 2 . x 3 ... x k) = zarejestruj x 1 + zarejestruj x 2 + zarejestruj x 3 + ... + zaloguj a x k.

Z twierdzenie o logarytmie ilorazowym możesz uzyskać jeszcze jedną właściwość logarytmu. Powszechnie wiadomo, że log a 1 = 0, zatem

Dziennik a 1 /b= log a 1 - log b= - log b.

Czyli równość ma miejsce:

zaloguj a 1 / b = - zaloguj a b.

Logarytmy dwóch wzajemnie odwrotnych liczb na tej samej podstawie będą się różnić od siebie wyłącznie znakiem. Więc:

Log 3 9 = - log 3 1/9; log 5 1/125 = -log 5 125.

Logarytm liczby n z powodu a zwany wykładnikiem NS do którego chcesz zbudować a zdobyć numer n

Pod warunkiem że
,
,

Z definicji logarytmu wynika, że:
, tj.
- ta równość jest podstawową tożsamością logarytmiczną.

Logarytmy o podstawie 10 nazywane są logarytmami dziesiętnymi. Zamiast
pisać
.

Logarytmy do podstawy mi nazywane są naturalnymi i są oznaczone
.

Podstawowe własności logarytmów.

Logarytm jedynki dla dowolnej podstawy wynosi zero

Logarytm iloczynu jest równy sumie logarytmów czynników.

3) Logarytm ilorazu jest równy różnicy logarytmów

Czynnik
nazywany modułem przejścia z logarytmów u podstawy a do logarytmów na podstawie b .

Korzystając z właściwości 2-5, często można zredukować logarytm złożonego wyrażenia do wyniku prostych operacji arytmetycznych na logarytmach.

Na przykład,

Takie przekształcenia logarytmu nazywamy logarytmem. Transformacje odwrotne do logarytmu nazywane są wzmacnianiem.

Rozdział 2. Elementy matematyki wyższej.

1. Ograniczenia

Granica funkcji
jest skończoną liczbą A jeśli, gdy podchodzisz xx 0 dla każdego presetu
, jest taka liczba
że raz
, następnie
.

Funkcja, która ma limit, różni się od niego o nieskończenie małą wartość:
, gdzie jest b.m.v., czyli
.

Przykład. Rozważ funkcję
.

Kiedy starasz się
, funkcja tak dąży do zera:

1.1. Podstawowe twierdzenia o granicach.

Granica stałej wartości jest równa tej stałej wartości

.

Granica sumy (różnicy) skończonej liczby funkcji jest równa sumie (różnicy) granic tych funkcji.

Granica iloczynu skończonej liczby funkcji jest równa iloczynowi granic tych funkcji.

Granica ilorazu dwóch funkcji jest równa ilorazowi granic tych funkcji, jeśli granica mianownika nie jest równa zeru.

Cudowne granice

,
, gdzie

1.2. Przykłady obliczeń granicznych

Jednak nie wszystkie limity są łatwe do obliczenia. Częściej obliczenie limitu sprowadza się do ujawnienia niepewności typu: lub .

.

2. Pochodna funkcji

Miejmy funkcję
ciągły na segmencie
.

Argument dostałem trochę przyrostu
... Wtedy funkcja otrzyma przyrost
.

Wartość argumentu odpowiada wartości funkcji
.

Wartość argumentu
odpowiada wartości funkcji.

Stąd, .

Znajdźmy granicę tego stosunku przy
... Jeśli ta granica istnieje, nazywa się ją pochodną tej funkcji.

Definicja 3 Pochodna tej funkcji
przez argument nazywamy granicą stosunku przyrostu funkcji do przyrostu argumentu, gdy przyrost argumentu arbitralnie dąży do zera.

Pochodna funkcji
można wyznaczyć w następujący sposób:

; ; ; .

Definicja 4 Operacja znajdowania pochodnej funkcji nazywa się różnicowanie.

2.1. Mechaniczne znaczenie pochodnej.

Rozważ prostoliniowy ruch jakiegoś sztywnego ciała lub punktu materialnego.

Niech w pewnym momencie ruchomy punkt
był na odległość od pozycji wyjściowej
.

Po pewnym czasie
przeszła na odległość
... Postawa =- średnia prędkość punktu materialnego
... Znajdźmy granicę tego stosunku, biorąc pod uwagę, że
.

W konsekwencji definicja chwilowej prędkości ruchu punktu materialnego sprowadza się do znalezienia pochodnej drogi w czasie.

2.2. Pochodna wartość geometryczna

Miejmy graficznie podaną jakąś funkcję
.

Ryż. 1. Geometryczne znaczenie pochodnej

Gdyby
następnie wskaż
, będzie poruszać się po łuku, zbliżając się do punktu
.

Stąd
, tj. wartość pochodnej przy podanej wartości argumentu liczbowo równa stycznej kąta utworzonego przez styczną w danym punkcie z dodatnim kierunkiem osi
.

2.3. Tabela podstawowych wzorów różniczkowania.

Funkcja zasilania

Funkcja wykładnicza

Funkcja logarytmiczna

Funkcja trygonometryczna

Odwrotna funkcja trygonometryczna

2.4. Zasady różnicowania.

Pochodzi z

Pochodna sumy (różnicy) funkcji

Pochodna iloczynu dwóch funkcji

Pochodna ilorazu dwóch funkcji

2.5. Pochodzi ze złożonej funkcji.

Biorąc pod uwagę funkcję
tak, że można go przedstawić jako

oraz
gdzie zmienna jest argumentem pośrednim, więc

Pochodna funkcji zespolonej jest równa iloczynowi pochodnej tej funkcji względem argumentu pośredniego przez pochodną argumentu pośredniego względem x.

Przykład 1.

Przykład 2.

3. Funkcja różniczkowa.

Niech będzie
różniczkowalny na pewnym segmencie
Odpuść sobie w ta funkcja ma pochodną

,

wtedy możemy pisać

(1),

gdzie - nieskończenie mała wartość,

od w

Mnożenie wszystkich warunków równości (1) przez
mamy:

Gdzie
- b.m.w. wyższego rzędu.

Ilość
nazywana jest różniczką funkcji
i oznaczone

.

3.1. Wartość geometryczna różniczki.

Biorąc pod uwagę funkcję
.

Rys. 2. Geometryczne znaczenie różniczki.

.

Oczywiście, różniczka funkcji
jest równy przyrostowi rzędnej stycznej w tym punkcie.

3.2. Pochodne i różniczki różnych rzędów.

Jeśli jest
, następnie
nazwany pierwszą pochodną.

Pochodna pierwszej pochodnej nazywana jest pochodną drugiego rzędu i jest zapisana
.

Pochodna n-tego rzędu funkcji
pochodna (n-1) -tego rzędu jest wywoływana i zapisywana:

.

Różniczka różniczki funkcji nazywana jest różniczką drugiego rzędu lub różniczką drugiego rzędu.

.

.

3.3 Rozwiązywanie problemów biologicznych za pomocą różnicowania.

Zadanie 1. Badania wykazały, że wzrost kolonii mikroorganizmów jest zgodny z prawem
, gdzie n - liczba mikroorganizmów (w tysiącach), T –Czas (dni).

b) Czy w tym okresie wielkość kolonii zwiększy się czy zmniejszy?

Odpowiedź. Kolonia powiększy się.

Zadanie 2. Woda w jeziorze jest okresowo badana pod kątem zawartości bakterii chorobotwórczych. Przez T dni po badaniu stężenie bakterii jest określone przez stosunek

.

Kiedy w jeziorze pojawi się minimalne stężenie bakterii i będzie można w nim pływać?

ROZWIĄZANIE Funkcja osiąga max lub min, gdy jej pochodna wynosi zero.

,

Zdefiniujmy max lub min będzie za 6 dni. W tym celu bierzemy drugą pochodną.

Odpowiedź: Po 6 dniach będzie minimalne stężenie bakterii.

Definicja logarytmu

Logarytm b przy podstawie a jest wykładnikiem, do którego należy podnieść a, aby uzyskać b.

Numer e w matematyce zwyczajowo oznacza się granicę, do której powinno dążyć wyrażenie

Numer e jest liczba niewymierna- liczba niewspółmierna do jednostki, nie może być dokładnie wyrażona jako całość lub ułamek racjonalny numer.

List mi- pierwsza litera słowa łacińskiego wykładnik- afiszować, stąd nazwa w matematyce wykładniczy- funkcja wykładnicza.

Numer mi szeroko stosowane w matematyce i we wszystkich naukach, w taki czy inny sposób wykorzystując obliczenia matematyczne dla swoich potrzeb.

Logarytmy. Własności logarytmów

Definicja: Podstawowym logarytmem liczby dodatniej b jest wykładnik c, do którego liczba a musi zostać podniesiona, aby otrzymać liczbę b.

Podstawowa tożsamość logarytmiczna:

7) Wzór przejścia na nową bazę:

lna = log e a, e ≈ 2,718 ...

Problemy i testy na temat „Logarytmy. Własności logarytmów”

• Logarytmy — ważne tematy dotyczące przeglądu ujednoliconego egzaminu państwowego z matematyki

Aby pomyślnie wykonać zadania na ten temat, musisz znać definicję logarytmu, właściwości logarytmów, podstawową tożsamość logarytmiczną, definicje logarytmu dziesiętnego i naturalnego. Głównymi rodzajami problemów na ten temat są problemy obliczania i przekształcania wyrażeń logarytmicznych. Rozważmy ich rozwiązanie w poniższych przykładach.

Rozwiązanie: Korzystając z własności logarytmów otrzymujemy

Rozwiązanie: korzystając z właściwości stopnia otrzymujemy

1) (2 2) log 2 5 = (2 log 2 5) 2 = 5 2 = 25

Własności logarytmów, sformułowań i dowodów.

Logarytmy mają szereg charakterystycznych właściwości. W tym artykule omówimy główne własności logarytmów... Tutaj podajemy ich sformułowania, wypisujemy własności logarytmów w postaci wzorów, pokazujemy przykłady ich zastosowania, a także podajemy dowody własności logarytmów.

Nawigacja po stronach.

Podstawowe własności logarytmów, wzory

Dla ułatwienia zapamiętywania i użytkowania reprezentujemy podstawowe własności logarytmów jako lista formuł. W następnym akapicie podamy ich sformułowania, dowody, przykłady użycia i niezbędne wyjaśnienia.

Własność logarytmu jedności: log a 1 = 0 dla dowolnego a> 0, a ≠ 1.

Logarytm liczby o podstawie: log a a = 1 dla a> 0, a ≠ 1.

Własność logarytmu stopnia podstawy: log a a p = p, gdzie a> 0, a ≠ 1 i p jest dowolną liczbą rzeczywistą.

Logarytm iloczynu dwóch liczb dodatnich: log a (x y) = log a x + log a y, a> 0, a 1, x> 0, y> 0,
oraz własność logarytmu iloczynu n liczb dodatnich: log a (x 1 x 2… xn) = log ax 1 + log ax 2 +… + log axn, a> 0, a ≠ 1, x 1> 0 , x 2 > 0,…, xn> 0.

Własność logarytmiczna ilorazu: , gdzie a> 0, a 1, x> 0, y> 0.

Logarytm potęgi liczby: log a b p = p · log a | b | , gdzie a> 0, a ≠ 1, b i p są liczbami takimi, że stopień bp ma sens i bp> 0.

Następstwo: , gdzie a> 0, a ≠ 1, n jest liczbą naturalną większą od jeden, b> 0.

Wniosek 1: , a> 0, a 1, b> 0, b ≠ 1.

Wniosek 2: , a> 0, a ≠ 1, b> 0, p i q są liczbami rzeczywistymi, q ≠ 0, w szczególności dla b = a mamy .

Oświadczenia i dowody właściwości

Przechodzimy do sformułowania i dowodu zarejestrowanych własności logarytmów. Wszystkie własności logarytmów są udowadniane na podstawie definicji logarytmu i wynikającej z niego głównej tożsamości logarytmicznej oraz własności stopnia.

Zacznijmy własności logarytmu jedności... Jego sformułowanie jest następujące: logarytm jedynki wynosi zero, to znaczy log a 1 = 0 dla dowolnego a> 0, a 1. Dowód jest prosty: ponieważ a 0 = 1 dla dowolnego a spełniającego powyższe warunki a> 0 i a ≠ 1, udowodniony log równości a 1 = 0 wynika bezpośrednio z definicji logarytmu.

Podajmy przykłady zastosowania rozważanej właściwości: log 3 1 = 0, lg1 = 0 i.

Przechodząc do następnej nieruchomości: logarytm liczby podstawowej to jeden, to jest, log a a = 1 dla a> 0, a 1. Rzeczywiście, skoro a 1 = a dla dowolnego a, to z definicji logarytmu logarytm a a = 1.

Przykładami użycia tej własności logarytmów są równości log 5 5 = 1, log 5,6 5,6 i lne = 1.

Logarytm potęgi liczby równej podstawie logarytmu jest równy wykładnikowi... Ta własność logarytmu odpowiada formule postaci log a a p = p, gdzie a> 0, a ≠ 1 i p jest dowolną liczbą rzeczywistą. Ta własność wynika bezpośrednio z definicji logarytmu. Zwróć uwagę, że pozwala od razu wskazać wartość logarytmu, jeśli możliwe jest przedstawienie liczby pod znakiem logarytmu w postaci stopnia podstawy, więcej o tym porozmawiamy w artykule obliczanie logarytmów.

Na przykład log 2 2 7 = 7, lg10 -4 = -4 i .

Logarytm iloczynu dwóch liczb dodatnich x i y są równe iloczynowi logarytmów tych liczb: log a (x y) = log a x + log a y, a> 0, a 1. Wykażmy własność logarytmu iloczynu. Na mocy własności stopnia log a x + log ay = log ax a log ay, a ponieważ z podstawowej tożsamości logarytmicznej log ax = x i log ay = y, to log ax y. Zatem log a x + log a y = x

Pokażmy przykłady wykorzystania własności logarytmu iloczynu: log 5 (2 3) = log 5 2 + log 5 3 i .

Własność logarytmu iloczynu można uogólnić na iloczyn skończonej liczby n liczb dodatnich x 1, x 2, ..., x n jako log a (x 1 x 2… x n) = log a x 1 + log a x 2 +… + log a x n... Równość tę można bez problemu udowodnić metodą indukcji matematycznej.

Na przykład logarytm naturalny iloczynu można zastąpić sumą trzech logarytmów naturalnych liczb 4, e, i.

Logarytm ilorazu dwóch liczb dodatnich x i y są równe różnicy między logarytmami tych liczb. Własność logarytmu ilorazu odpowiada formule postaci , gdzie a> 0, a ≠ 1, x i y są liczbami dodatnimi. Udowodniono słuszność tego wzoru oraz wzoru na logarytm iloczynu: od , to z definicji logarytmu .

Oto przykład użycia tej właściwości logarytmu: .

Przejść do własność logarytmu stopnia... Logarytm potęgi jest równy iloczynowi wykładnika przez logarytm modułu podstawy tej potęgi. Tę właściwość logarytmu stopnia zapisujemy w postaci wzoru: log a b p = p · log a | b |, gdzie a> 0, a ≠ 1, b i p są liczbami takimi, że stopień bp ma sens i bp> 0.

Najpierw udowadniamy tę właściwość dla pozytywnego b. Główna tożsamość logarytmiczna pozwala nam przedstawić liczbę b jako log a b, następnie bp = (a log a b) p, a wynikowe wyrażenie, ze względu na właściwość stopnia, jest równe a p log a b. Dochodzimy więc do równości b p = a p log a b, z której, z definicji logarytmu, wnioskujemy, że log a bp = p log a b.

Pozostaje udowodnić tę właściwość dla ujemnego b. Tutaj zauważamy, że wyrażenie log a bp dla ujemnego b ma sens tylko dla parzystych wykładników p (ponieważ wartość wykładnika bp musi być większa od zera, w przeciwnym razie logarytm nie będzie miał sensu), a w tym przypadku b p = | b | P. Wtedy b p = | b | p = (a log a | b |) p = a p · log a | b | , skąd log a b p = p · log a | b | ...

Na przykład, oraz ln(-3) 4 = 4 ln|-3|=4 ln3.

Poprzednia właściwość implikuje właściwość logarytmu z rdzenia: logarytm n-tego pierwiastka jest równy iloczynowi ułamka 1 / n przez logarytm radykalnego wyrażenia, to znaczy, gdzie a> 0, a ≠ 1, n jest liczbą naturalną większą niż jeden, b> 0 .

Dowód opiera się na równości (patrz definicja wykładnika ułamkowego), która jest prawdziwa dla każdego dodatniego b, oraz własności logarytmu wykładnika: .

Oto przykład z wykorzystaniem tej właściwości: .

Teraz pozwól nam udowodnić wzór na przejście do nowej podstawy logarytmu uprzejmy ... Aby to zrobić, wystarczy udowodnić log równości c b = log a b log c a. Główna tożsamość logarytmiczna pozwala nam reprezentować liczbę b jako log a b, a następnie log c b = log c a log a b. Pozostaje wykorzystać własność logarytmu stopnia: log c a log a b = log a b log c a. To dowodzi, że log c b = log a b log c a, co oznacza, że ​​wzór na przejście do nowej podstawy logarytmu jest również udowodniony .

Pokażmy kilka przykładów zastosowania tej własności logarytmów: i .

Formuła przejścia do nowej podstawy pozwala przejść do pracy z logarytmami, które mają „wygodną” podstawę. Na przykład możesz go użyć, aby przejść do logarytmów naturalnych lub dziesiętnych, aby obliczyć wartość logarytmu z tabeli logarytmów. Wzór na przejście do nowej podstawy logarytmu pozwala również w niektórych przypadkach znaleźć wartość danego logarytmu, gdy znane są wartości niektórych logarytmów o innych podstawach.

Często stosuje się specjalny przypadek wzoru na przejście do nowej podstawy logarytmu z c = b postaci. To pokazuje, że log a b i log b a są liczbami wzajemnie odwrotnymi. Na przykład, .

Często używana jest również formuła, która jest wygodna do znajdowania wartości logarytmów. Aby potwierdzić nasze słowa, pokażemy, w jaki sposób jest używany do obliczenia wartości logarytmu formularza. Mamy ... Do udowodnienia wzoru wystarczy posłużyć się wzorem na przejście do nowej podstawy logarytmu a: .

Pozostaje udowodnić właściwości porównania logarytmów.

Użyjmy metody przez sprzeczność. Załóżmy, że dla a 1> 1, a 2> 1 i a 1 2 oraz dla 0 1 log a 1 b≤log a 2 b. Dzięki własnościom logarytmów nierówności te można przepisać jako oraz i z nich wynika, że ​​odpowiednio log b a 1 ≤ log b a 2 i log b a 1 ≥ log b a 2. Następnie, zgodnie z własnościami stopni o tych samych podstawach, powinny obowiązywać równości b log b a 1 ≥ b log b a 2 i b log b a 1 ≥ b log b a 2, czyli a 1 ≥ a 2. W ten sposób doszliśmy do sprzeczności z warunkiem a 1 2. To kończy dowód.

Podstawowe własności logarytmów

• Materiały lekcyjne
• Pobierz wszystkie formuły

Logarytmy, podobnie jak wszystkie liczby, można dodawać, odejmować i przekształcać w dowolny sposób. Ale ponieważ logarytmy nie są zwykłymi liczbami, istnieją tutaj reguły, które nazywają się podstawowe właściwości.

Znajomość tych zasad jest konieczna – bez nich nie można rozwiązać żadnego poważnego problemu logarytmicznego. W dodatku jest ich bardzo mało – wszystkiego można się nauczyć w jeden dzień. Więc zacznijmy.

Dodawanie i odejmowanie logarytmów

Rozważmy dwa logarytmy o tych samych podstawach: log ax i log ay. Następnie można je dodawać i odejmować oraz:

Zatem suma logarytmów jest równa logarytmowi iloczynu, a różnica jest logarytmem ilorazu. Pamiętaj, że kluczową kwestią jest tutaj: identyczne podstawy... Jeśli powody są różne, te zasady nie działają!

Te formuły pomogą Ci obliczyć wyrażenie logarytmiczne, nawet jeśli jego poszczególne części nie są liczone (zobacz lekcję „Co to jest logarytm”). Spójrz na przykłady - i zobacz:

Zadanie. Znajdź wartość wyrażenia: log 6 4 + log 6 9.

Ponieważ podstawy logarytmów są takie same, używamy wzoru sumy:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Zadanie. Znajdź wartość wyrażenia: log 2 48 - log 2 3.

Bazy są takie same, stosujemy wzór różnicy:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Zadanie. Znajdź wartość wyrażenia: log 3 135 - log 3 5.

Znowu podstawy są takie same, więc mamy:
log 3 135 - log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Jak widać, oryginalne wyrażenia składają się ze „złych” logarytmów, które nie są oddzielnie liczone. Ale po przekształceniach otrzymuje się całkiem normalne liczby. Wiele testów opiera się na tym fakcie. Ale jaka kontrola - takie wyrażenia z całą powagą (czasami - praktycznie niezmienione) są oferowane na egzaminie.

Usunięcie wykładnika z logarytmu

Teraz trochę skomplikujmy zadanie. Co się stanie, jeśli podstawa lub argument logarytmu opiera się na stopniu? Następnie wykładnik tego stopnia można wyciągnąć ze znaku logarytmu według następujących zasad:

• log a x n = n log a x;
• 
• 

Łatwo zauważyć, że ostatnia zasada jest zgodna z dwoma pierwszymi. Ale lepiej o tym pamiętać - w niektórych przypadkach znacznie zmniejszy to ilość obliczeń.

Oczywiście wszystkie te reguły mają sens, jeśli przestrzegany jest ODL logarytmu: a> 0, a ≠ 1, x> 0. I jeszcze jedno: naucz się stosować wszystkie formuły nie tylko od lewej do prawej, ale także na odwrót , tj możesz wpisać liczby przed znakiem logarytmu do samego logarytmu. To jest najczęściej wymagane.

Zadanie. Znajdź wartość wyrażenia: log 7 49 6.

Pozbądźmy się stopnia w argumencie za pomocą pierwszej formuły:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Zadanie. Znajdź znaczenie wyrażenia:

[Podpis pod rysunkiem]

Zauważ, że mianownik zawiera logarytm, którego podstawą i argumentem są dokładne potęgi: 16 = 2 4; 49 = 7 2. Mamy:

[Podpis pod rysunkiem]

Myślę, że ostatni przykład wymaga wyjaśnienia. Gdzie zniknęły logarytmy? Do ostatniej chwili pracujemy tylko z mianownikiem. Przedstawiliśmy podstawę i argument stojącego tam logarytmu w postaci stopni i wydobyliśmy wskaźniki - otrzymaliśmy ułamek „trzypiętrowy”.

Spójrzmy teraz na ułamek podstawowy. Licznik i mianownik zawierają tę samą liczbę: log 2 7. Ponieważ log 2 7 ≠ 0 możemy skreślić ułamek - mianownik pozostaje 2/4. Zgodnie z zasadami arytmetyki czwórkę można przenieść do licznika, co zostało zrobione. Rezultatem była odpowiedź: 2.

Przeprowadzka do nowej fundacji

Mówiąc o zasadach dodawania i odejmowania logarytmów, szczególnie podkreśliłem, że działają one tylko dla tych samych podstaw. A jeśli powody są inne? A co, jeśli nie są to dokładne potęgi o tej samej liczbie?

Na ratunek przychodzą formuły przejścia na nowy fundament. Sformułujmy je w postaci twierdzenia:

Niech będzie dany logarytm logarytmujący x. Wtedy dla dowolnej liczby c takiej, że c> 0 i c ≠ 1, zachodzi następująca równość:

[Podpis pod rysunkiem]

W szczególności, jeśli postawimy c = x, otrzymamy:

[Podpis pod rysunkiem]

Z drugiej formuły wynika, że ​​można zamienić podstawę i argument logarytmu, ale w tym przypadku całe wyrażenie jest „odwrócone”, tj. logarytm pojawia się w mianowniku.

Te formuły rzadko występują w konwencjonalnych wyrażeniach liczbowych. Można oszacować, jak wygodne są one tylko przy rozwiązywaniu równań logarytmicznych i nierówności.

Istnieją jednak zadania, które zazwyczaj nie są rozwiązywane z wyjątkiem przejścia do nowej fundacji. Rozważ kilka z nich:

Zadanie. Znajdź wartość wyrażenia: log 5 16 log 2 25.

Zauważ, że argumenty obu logarytmów zawierają dokładne stopnie. Wyjmijmy wskaźniki: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Teraz „odwróćmy” drugi logarytm:

[Podpis pod rysunkiem]

Ponieważ iloczyn nie zmienia się z permutacji czynników, spokojnie pomnożyliśmy cztery i dwa, a następnie zajęliśmy się logarytmami.

Zadanie. Znajdź wartość wyrażenia: log 9 100 · lg 3.

Podstawą i argumentem pierwszego logarytmu są dokładne stopnie. Zapiszmy to i pozbądźmy się metryk:

[Podpis pod rysunkiem]

Pozbądźmy się teraz logarytmu dziesiętnego, przechodząc do nowej podstawy:

[Podpis pod rysunkiem]

Podstawowa tożsamość logarytmiczna

Często w procesie rozwiązywania wymagane jest przedstawienie liczby jako logarytmu do danej podstawy. W takim przypadku pomogą nam formuły:

1. n = log a a n

2. W pierwszym przypadku liczba n staje się wykładnikiem w argumencie. Liczba n może być absolutnie dowolna, ponieważ jest to po prostu wartość logarytmu.

   Druga formuła jest właściwie sparafrazowaną definicją. Nazywa się to: podstawową tożsamością logarytmiczną.

   Rzeczywiście, co się stanie, jeśli liczba b zostanie podniesiona do takiej potęgi, że liczba b do tej potęgi daje liczbę a? Zgadza się: otrzymujesz ten sam numer a. Przeczytaj uważnie ten akapit jeszcze raz - wiele osób "wisi" na nim.

   Podobnie jak formuły przejścia do nowej bazy, podstawowa tożsamość logarytmiczna jest czasami jedynym możliwym rozwiązaniem.

   [Podpis pod rysunkiem]

   Zauważ, że log 25 64 = log 5 8 - po prostu przesunąłeś kwadrat z podstawy i argumentu logarytmu. Biorąc pod uwagę zasady mnożenia stopni o tej samej podstawie, otrzymujemy:

   [Podpis pod rysunkiem]

   Jeśli ktoś nie wie, to był prawdziwy problem z egzaminu 🙂

   Jednostka logarytmiczna i zero logarytmiczne

   Na zakończenie podam dwie tożsamości, które trudno nazwać własnościami – są to raczej konsekwencje definicji logarytmu. Nieustannie napotykają na problemy i, co zaskakujące, stwarzają problemy nawet „zaawansowanym” studentom.

   1. log a a = 1 jest jednostką logarytmiczną. Pamiętaj raz na zawsze: logarytm dowolnej podstawy a z tej podstawy jest równy jeden.
   2. log a 1 = 0 to logarytmiczne zero. Podstawą a może być dowolna, ale jeśli argument jest jeden, logarytm wynosi zero! Ponieważ 0 = 1 jest bezpośrednią konsekwencją definicji.

   To wszystkie właściwości. Pamiętaj, aby przećwiczyć wprowadzanie ich w życie! Pobierz ściągawkę na początku lekcji, wydrukuj ją i rozwiąż problemy.

   Logarytm. Własności logarytmiczne (dodawanie i odejmowanie).

   Własności logarytmiczne wynikają z jego definicji. A więc logarytm liczby b z powodu a jest definiowany jako wskaźnik stopnia, w jakim liczba musi zostać podniesiona a zdobyć numer b(Logarytm istnieje tylko dla liczb dodatnich).

   Z tego sformułowania wynika, że ​​obliczenia x = log a b, jest równoważne rozwiązaniu równania a x = b. Na przykład, log 2 8 = 3 ponieważ 8 = 2 3 ... Sformułowanie logarytmu pozwala wykazać, że jeśli b = a c, to logarytm liczby b z powodu a jest równe z... Jasne jest również, że temat logarytmu jest ściśle związany z tematem potęgi liczby.

   Z logarytmami, jak z dowolnymi liczbami, możesz to zrobić operacje dodawania, odejmowania i przekształcać się w każdy możliwy sposób. Ale ze względu na to, że logarytmy nie są zwykłymi liczbami, obowiązują tutaj specjalne zasady, które nazywają się podstawowe właściwości.

   Dodawanie i odejmowanie logarytmów.

   Weźmy dwa logarytmy o tych samych podstawach: zarejestruj x oraz zaloguj się... Następnie usuń możliwe jest wykonywanie operacji dodawania i odejmowania:

   Jak widzisz suma logarytmów równa się logarytmowi iloczynu, a różnica logarytmy- logarytm ilorazu. Co więcej, jest to prawdą, jeśli liczby a, NS oraz w pozytywne i 1.

   Ważne jest, aby zwrócić uwagę na fakt, że głównym aspektem w tych formułach są te same podstawy. Jeśli podstawy różnią się od siebie, zasady te nie mają zastosowania!

   Zasady dodawania i odejmowania logarytmów o tych samych podstawach są odczytywane nie tylko od lewej do prawej, ale także od tyłu. W rezultacie mamy twierdzenia o logarytmie iloczynu i logarytmie ilorazu.

   Logarytm produktu dwie liczby dodatnie są równe sumie ich logarytmów ; parafrazując to twierdzenie, jeśli liczby a, x oraz w pozytywne i 1, następnie:

   Logarytm ilorazu dwie liczby dodatnie są równe różnicy między logarytmami dzielnej i dzielnika. Innymi słowy, jeśli liczby a, NS oraz w pozytywne i 1, następnie:

   Do rozwiązania stosujemy powyższe twierdzenia przykłady:

   Jeśli liczby x oraz w negatywne, to wzór na logarytm iloczynu staje się bez znaczenia. Zabronione jest więc pisanie:

   ponieważ wyrażenia log 2 (-8) i log 2 (-4) w ogóle nie są zdefiniowane (funkcja logarytmiczna) w= log 2 NS zdefiniowany tylko dla dodatnich wartości argumentu NS).

   Twierdzenie o produkcie dotyczy nie tylko dwóch, ale także nieograniczonej liczby czynników. Oznacza to, że dla każdego naturalnego k i wszelkie liczby dodatnie x 1 , x 2 , . . . ,x n istnieje tożsamość:

   Z twierdzenie o logarytmie ilorazowym możesz uzyskać jeszcze jedną właściwość logarytmu. Powszechnie wiadomo, że log a 1 = 0, zatem

   Czyli równość ma miejsce:

   Logarytmy dwóch wzajemnie odwrotnych liczb na tej samej podstawie będą się różnić od siebie wyłącznie znakiem. Więc:

   Logarytm. Własności logarytmów

   Logarytm. Własności logarytmów

   Rozważ równość. Daj nam znać wartości i a my chcemy znaleźć wartość.

   Oznacza to, że szukamy wykładnika stopnia, w jakim musimy się napinać, aby uzyskać.

   Zostawiać zmienna może przyjąć dowolną poprawną wartość, wówczas na zmienne nakładane są następujące ograniczenia: o "title =" a> o "/>, 1 ″ tytuł = ” a1 ″ />, 0 ″ tytuł = ”b> 0 ″ / >

   Jeśli znamy wartości i i stoimy przed zadaniem znalezienia nieznanego, to w tym celu wprowadza się działanie matematyczne, które nazywa się logarytm.

   Aby znaleźć znaczenie, bierzemy logarytm liczby na podstawa :

   Logarytm liczby do podstawy jest wykładnikiem, do którego należy ją podnieść, aby uzyskać.

   To jest podstawowa tożsamość logarytmiczna:

   o "tytuł =" a> o "/>, 1 ″ tytuł = ” a1 ″ />, 0 ″ tytuł = ”b> 0 ″ />

   jest zasadniczo notacją matematyczną definicja logarytmu.

   Operacja matematyczna logarytmująca jest odwrotnością operacji potęgowania, dlatego własności logarytmówściśle związane z właściwościami stopnia.

   Wymieńmy główne własności logarytmów:

   (o "tytuł =" a> o "/>, 1 ″ tytuł = ” a1 ″ />, 0 ″ tytuł = ”b> 0 ″ />, 0,

   d> 0 ″ />, 1 ″ tytuł = ”d1 ″ />

   4.

   5.

   Kolejna grupa własności pozwala przedstawić wykładnik wyrażenia pod znakiem logarytmu lub u podstawy logarytmu jako współczynnik przed znakiem logarytmu:

   6.

   7.

   8.

   9.

   Kolejna grupa formuł pozwala przejść od logarytmu o zadanej podstawie do logarytmu o dowolnej podstawie i nosi nazwę formuły przejścia:

   10.

   12. (następstwo z własności 11)

   

   Poniższe trzy właściwości nie są zbyt dobrze znane, ale są często używane przy rozwiązywaniu równań logarytmicznych lub przy upraszczaniu wyrażeń zawierających logarytmy:

   13.

   14.

   15.

   Przypadki specjalne:

   — logarytm dziesiętny

   — naturalny logarytm

   Przy upraszczaniu wyrażeń zawierających logarytmy stosuje się podejście ogólne:

   1. Reprezentujemy ułamki dziesiętne w postaci zwykłych.

   2. Liczby mieszane reprezentujemy jako ułamki niewłaściwe.

   3. Liczby u podstawy logarytmu i pod znakiem logarytmu są rozkładane na czynniki pierwsze.

   4. Staramy się sprowadzić wszystkie logarytmy do jednej podstawy.

   5. Zastosuj własności logarytmów.

   Spójrzmy na kilka przykładów uproszczenia wyrażeń zawierających logarytmy.

   Przykład 1.

   Oblicz:

   Uprośćmy wszystkie wykładniki: naszym zadaniem jest sprowadzenie ich do logarytmów, których podstawa jest taka sama jak podstawa stopnia.

   == (według właściwości 7) = (według właściwości 6) =

   Zastąpmy wskaźniki, które otrzymaliśmy w oryginalnym wyrażeniu. Otrzymujemy:

   Odpowiedź: 5.25

   Przykład 2. Oblicz:

   

   Sprowadźmy wszystkie logarytmy do podstawy 6 (w tym przypadku logarytmy z mianownika ułamka „przeniosą się” do licznika):

   Rozłóżmy liczby pod logarytmem na czynniki pierwsze:

   Zastosujmy właściwości 4 i 6:

   Przedstawmy zamiennik

   Otrzymujemy:

   Odpowiedź 1

   Logarytm . Podstawowa tożsamość logarytmiczna.

   Własności logarytmów. Logarytm dziesiętny. Naturalny logarytm.

   Logarytm liczba dodatnia N przez podstawę (b > 0, b 1) jest wykładnikiem x, do którego należy podnieść b, aby uzyskać N .

   Ten wpis jest odpowiednikiem następującego: b x = N .

   Przykłady: log 3 81 = 4, ponieważ 3 4 = 81;

   log 1/3 27 = – 3, ponieważ (1/3) - 3 = 3 3 = 27.

   Powyższą definicję logarytmu można zapisać jako tożsamość:

   

   Podstawowe własności logarytmów.

   2) log 1 = 0, ponieważ b 0 = 1 .

   3) Logarytm iloczynu jest równy sumie logarytmów czynników:

   4) Logarytm ilorazu jest równy różnicy między logarytmami dywidendy a dzielnikiem:

   5) Logarytm potęgi jest równy iloczynowi wykładnika przez logarytm jego podstawy:

   Konsekwencją tej właściwości jest: logarytm pierwiastkowy jest równa logarytmowi liczby pierwiastkowej podzielonej przez potęgę pierwiastka:

   

   6) Jeśli u podstawy logarytmu znajduje się stopień, to wartość odwrotność wykładnika wykładnika może być wyjęta dla znaku rymów logarytmicznych:

   

   Dwie ostatnie właściwości można połączyć w jedną:

   

   7) Wzór na moduł przejścia (tj. przejście od jednej podstawy logarytmu do innej podstawy):

   

   W konkretnym przypadku dla N = a mamy:

   

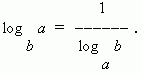
   Logarytm dziesiętny nazywa logarytm do podstawy 10. Jest oznaczony jako lg, tj. log 10 n= lg n... Logarytmy liczb 10, 100, 1000. p avna odpowiednio 1, 2, 3, ..., tj. mieć tak wiele pozytywnych

   jednostki, ile zer jest w logarytmie po jedynce. Logarytmy liczb 0,1, 0,01, 0,001,. p to odpowiednio –1, –2, –3,…, tj. mieć tyle ujemnych jedynek, ile jest zer w logarytmie przed jedynką (liczba i zero liczb całkowitych). Logarytmy pozostałych liczb mają część ułamkową zwaną mantysa... Cała część logarytmu nazywa się Charakterystyka... Do praktycznego zastosowania najwygodniejsze są logarytmy dziesiętne.

   Naturalny logarytm nazywa logarytm do podstawy mi... Jest oznaczony przez ln, tj. Dziennik mi n= ln n... Numer mi jest irracjonalny, jego przybliżona wartość to 2.718281828. Jest to granica, do której liczba (1 + 1 / n) n z nieograniczonym wzrostem n(cm. pierwszy wspaniały limit(patrz strona Granice sekwencji liczb).
   Choć może się to wydawać dziwne, logarytmy naturalne okazały się bardzo wygodne przy wykonywaniu różnego rodzaju operacji związanych z analizą funkcji. Obliczanie logarytmów podstawowych mi odbywa się znacznie szybciej niż na jakiejkolwiek innej podstawie.

• Co jest dziś potrzebne do adopcji dziecka w Rosji? Adopcja w Rosji, oprócz odpowiedzialnej decyzji osobistej, obejmuje szereg procedur państwowej weryfikacji kandydatów. Rygorystyczna selekcja na etapie przygotowawczym przyczynia się do większej [...]
• Informacje bezpłatne na temat NIP lub OGRN z rejestru podatkowego w całej Rosji - online Na jednolitym portalu usług podatkowych informacje o rejestracji państwowej osób prawnych, indywidualnych przedsiębiorców, [...]
• Kara za jazdę bez dokumentów (prawo jazdy, ubezpieczenie, STS) Czasami z powodu zapomnienia kierowcy zasiadają za kierownicą bez VU i otrzymują mandat za jazdę bez dokumentów. Przypomnijmy, że miłośnik motoryzacji ma obowiązek z nim być [...]
• Kwiaty mężczyzn. Jakie kwiaty możesz dać mężczyźnie? Jakie kwiaty możesz dać mężczyźnie? Nie ma tak wielu „męskich” kolorów, ale są takie, które są dane mężczyznom. Przed tobą mała kwiecista lista: chryzantemy. Róże. Goździki. […]
• Notatka to specjalna forma dokumentu, która jest wykorzystywana w wewnętrznym środowisku przedsiębiorstwa i służy do szybkiego rozwiązywania bieżących problemów produkcyjnych. Zwykle dokument ten jest tworzony w celu wprowadzenia niektórych [...]
• Kiedy i jak uzyskać finansowaną część emerytury w Sbierbanku? Sberbank jest bankiem partnerskim państwowego funduszu emerytalnego. Na tej podstawie obywatele, którzy otrzymali emeryturę kapitałową mogli przenieść na nią część kapitałową [...]
• Świadczenia dla dzieci w Uljanowsku i regionie Uljanowsk w 2018 r. Ponadto we wszystkich regionach działają programy zatwierdzone przez ustawodawstwo federalne. Przeanalizujmy, kto może liczyć na jakie korzyści. Jako władze regionalne [...]
• Szczegółowe wskazówki, jak sporządzić pełnomocnictwo do reprezentowania interesów jednostki w sądzie W sprawie cywilnej lub arbitrażowej, w sprawie administracyjnej lub karnej interesy zarówno powoda, jak i pozwanego może reprezentować pełnomocnik: [...]