Farklı tabanlara sahip logaritmanın özelliklerine örnekler. Farklı tabanlı logaritmik denklemler. Logaritmanın temel özellikleri

Logaritmalar da diğer sayılar gibi her şekilde toplanabilir, çıkarılabilir ve dönüştürülebilir. Ancak logaritmalar tam olarak sıradan sayılar olmadığından burada kurallar vardır. ana özellikler.

Bu kuralları kesinlikle bilmeniz gerekir - onlar olmadan tek bir ciddi logaritmik problem çözülemez. Ayrıca bunlardan çok azı var - her şeyi bir günde öğrenebilirsiniz. Öyleyse başlayalım.

Logaritmaların toplanması ve çıkarılması

Aynı tabanlara sahip iki logaritmayı düşünün: log A X ve kayıt A sen. Daha sonra bunlar eklenebilir ve çıkarılabilir ve:

1. kayıt A X+ günlük A sen=günlük A (X · sen);
2. kayıt A X- günlük A sen=günlük A (X : sen).

Yani logaritmaların toplamı çarpımın logaritmasına, fark ise bölümün logaritmasına eşittir. Not: önemli an Burada - aynı gerekçeler. Sebepler farklıysa bu kurallar işe yaramaz!

Bu formüller, tek tek parçaları dikkate alınmasa bile logaritmik bir ifadeyi hesaplamanıza yardımcı olacaktır ("Logaritma nedir" dersine bakın). Örneklere bir göz atın ve şunu görün:

Günlük 6 4 + günlük 6 9.

Logaritmaların tabanları aynı olduğundan toplam formülünü kullanırız:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Görev. İfadenin değerini bulun: log 2 48 – log 2 3.

Bazlar aynı, fark formülünü kullanıyoruz:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Görev. İfadenin değerini bulun: log 3 135 – log 3 5.

Tabanlar yine aynı olduğundan elimizde:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Gördüğünüz gibi orijinal ifadeler ayrı olarak hesaplanmayan “kötü” logaritmalardan oluşuyor. Ancak dönüşümlerden sonra tamamen normal sayılar elde edilir. Birçoğu bu gerçek üzerine inşa edilmiştir sınav kağıtları. Evet, Birleşik Devlet Sınavında test benzeri ifadeler tüm ciddiyetiyle (bazen neredeyse hiç değişiklik yapılmadan) sunulmaktadır.

Üslü logaritmadan çıkarma

Şimdi görevi biraz karmaşıklaştıralım. Ya bir logaritmanın tabanı veya argümanı bir kuvvet ise? Daha sonra bu derecenin üssü aşağıdaki kurallara göre logaritmanın işaretinden çıkarılabilir:

Bunu fark etmek kolaydır son kural ilk ikisini takip ediyor. Ancak yine de hatırlamak daha iyidir - bazı durumlarda hesaplama miktarını önemli ölçüde azaltacaktır.

Elbette, logaritmanın ODZ'sine uyulduğu takdirde tüm bu kurallar anlamlıdır: A > 0, A ≠ 1, X> 0. Ve bir şey daha: tüm formülleri yalnızca soldan sağa değil, aynı zamanda tam tersi şekilde de uygulamayı öğrenin; Logaritma işaretinden önceki sayıları logaritmanın kendisine girebilirsiniz. En sık ihtiyaç duyulan şey budur.

Görev. İfadenin değerini bulun: log 7 49 6 .

İlk formülü kullanarak argümandaki dereceden kurtulalım:
günlük 7 49 6 = 6 günlük 7 49 = 6 2 = 12

Görev. İfadenin anlamını bulun:

[Resmin başlığı]

Paydanın, tabanı ve argümanının tam kuvvetleri olan bir logaritma içerdiğine dikkat edin: 16 = 2 4; 49 = 7 2. Sahibiz:

[Resmin başlığı]

sanırım son örnek açıklama gerekli. Logaritmalar nereye gitti? Son ana kadar sadece paydayla çalışıyoruz. Orada duran logaritmanın temelini ve argümanını kuvvetler şeklinde sunduk ve üsleri çıkardık - “üç katlı” bir kesir elde ettik.

Şimdi ana kesirlere bakalım. Pay ve payda aynı sayıyı içerir: log 2 7. Log 2 7 ≠ 0 olduğundan kesri azaltabiliriz - 2/4 paydada kalacaktır. Aritmetik kurallarına göre dörtlü paya aktarılabilir ki yapılan da budur. Sonuç şuydu: 2.

Yeni bir temele geçiş

Logaritma toplama ve çıkarma kurallarından bahsederken bunların sadece aynı tabanlarla çalıştığını özellikle vurguladım. Peki ya sebepler farklıysa? Ya aynı sayının tam kuvvetleri değilse?

Yeni bir vakfa geçiş formülleri kurtarmaya geliyor. Bunları bir teorem şeklinde formüle edelim:

Logaritma günlüğü verilsin A X. Daha sonra herhangi bir sayı için Cöyle ki C> 0 ve C≠ 1, eşitlik doğrudur:

[Resmin başlığı]

Özellikle şunu koyarsak C = X, şunu elde ederiz:

[Resmin başlığı]

İkinci formülden, logaritmanın tabanının ve argümanının değiştirilebileceği anlaşılmaktadır, ancak bu durumda ifadenin tamamı "tersine çevrilmiştir", yani. logaritma paydada görünür.

Bu formüllere sıradan sayısal ifadelerde nadiren rastlanır. Ne kadar kullanışlı olduklarını ancak logaritmik denklem ve eşitsizlikleri çözerken değerlendirmek mümkündür.

Ancak yeni bir temele taşınmak dışında hiçbir şekilde çözülemeyen sorunlar var. Bunlardan birkaçına bakalım:

Görev. İfadenin değerini bulun: log 5 16 log 2 25.

Her iki logaritmanın argümanlarının tam güçler içerdiğini unutmayın. Göstergeleri çıkaralım: log 5 16 = log 5 2 4 = 4log 5 2; günlük 2 25 = günlük 2 5 2 = 2 günlük 2 5;

Şimdi ikinci logaritmayı “tersine çevirelim”:

[Resmin başlığı]

Faktörleri yeniden düzenlerken çarpım değişmediğinden, sakince dört ve ikiyi çarptık ve ardından logaritmalarla uğraştık.

Görev. İfadenin değerini bulun: log 9 100 lg 3.

Birinci logaritmanın tabanı ve argümanı tam kuvvetlerdir. Bunu bir kenara yazalım ve göstergelerden kurtulalım:

[Resmin başlığı]

Şimdi yeni bir tabana geçerek ondalık logaritmadan kurtulalım:

[Resmin başlığı]

Temel logaritmik kimlik

Çoğu zaman çözüm sürecinde bir sayının belirli bir tabana göre logaritması olarak gösterilmesi gerekir. Bu durumda aşağıdaki formüller bize yardımcı olacaktır:

İlk durumda, sayı N argümandaki duruş derecesinin bir göstergesi haline gelir. Sayı N kesinlikle herhangi bir şey olabilir, çünkü bu yalnızca bir logaritma değeridir.

İkinci formül aslında başka kelimelerle ifade edilmiş bir tanımdır. Buna denir: temel logaritmik özdeşlik.

Aslında sayı gelse ne olur? Böyle bir güce yükseltin ki sayı B bu güce sayıyı verir A? Bu doğru: aynı numarayı alıyorsunuz A. Bu paragrafı dikkatlice tekrar okuyun; birçok kişi buna takılıp kalıyor.

Yeni bir tabana geçiş formülleri gibi, temel logaritmik özdeşlik de bazen mümkün olan tek çözümdür.

Görev. İfadenin anlamını bulun:

[Resmin başlığı]

Log 25 64 = log 5 8'in basitçe tabandan ve logaritmanın argümanından kareyi aldığını unutmayın. Aynı tabanla kuvvetleri çarpma kurallarını hesaba katarsak şunu elde ederiz:

[Resmin başlığı]

Bilmeyen varsa, bu Birleşik Devlet Sınavından gerçek bir görevdi :)

Logaritmik birim ve logaritmik sıfır

Sonuç olarak, özellik olarak adlandırılması pek mümkün olmayan iki kimlik vereceğim - bunlar daha ziyade logaritmanın tanımının sonuçlarıdır. Sürekli olarak sorunlarla karşılaşıyorlar ve şaşırtıcı bir şekilde "ileri düzey" öğrenciler için bile sorunlar yaratıyorlar.

1. kayıt A A= 1 logaritmik bir birimdir. Bir kez ve tamamen hatırlayın: herhangi bir tabana göre logaritma A bu tabandan itibaren bire eşittir.
2. kayıt A 1 = 0 logaritmik sıfırdır. Temel A herhangi bir şey olabilir, ancak argüman bir tane içeriyorsa - logaritma sıfıra eşit! Çünkü A 0 = 1 tanımın doğrudan bir sonucudur.

Tüm özellikler bu kadar. Bunları uygulamaya koymayı unutmayın! Dersin başındaki kopya kağıdını indirin, yazdırın ve problemleri çözün.

Talimatlar

Verilen logaritmik ifadeyi yazınız. İfade 10'un logaritmasını kullanıyorsa gösterimi kısaltılır ve şu şekilde görünür: lg b ondalık logaritmadır. Logaritmanın temelinde e sayısı varsa, şu ifadeyi yazın: ln b – doğal logaritma. Herhangi birinin sonucunun, b sayısını elde etmek için temel sayının yükseltilmesi gereken kuvvet olduğu anlaşılmaktadır.

İki fonksiyonun toplamını bulurken, tek tek türevlerini alıp sonuçları eklemeniz yeterlidir: (u+v)" = u"+v";

İki fonksiyonun çarpımının türevini bulurken, birinci fonksiyonun türevini ikinciyle çarpmak ve ikinci fonksiyonun türevinin birinci fonksiyonla çarpımını eklemek gerekir: (u*v)" = u"*v +v"*u;

İki fonksiyonun bölümünün türevini bulmak için, bölen fonksiyonu ile bölünen türevinin çarpımından bölen türevinin çarpımı ile bölünen fonksiyonun çarpımını çıkarmak ve bölmek gerekir. tüm bunlar bölen fonksiyonunun karesine göre. (u/v)" = (u"*v-v"*u)/v^2;

Karmaşık bir fonksiyon verilmişse türevini çarpmak gerekir. dahili fonksiyon ve dıştakinin türevi. y=u(v(x)) olsun, sonra y"(x)=y"(u)*v"(x) olsun.

Yukarıda elde edilen sonuçları kullanarak hemen hemen her işlevi ayırt edebilirsiniz. O halde birkaç örneğe bakalım:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2) *X));
Bir noktadaki türevin hesaplanmasıyla ilgili problemler de vardır. y=e^(x^2+6x+5) fonksiyonu verilsin, x=1 noktasında fonksiyonun değerini bulmanız gerekiyor.
1) Fonksiyonun türevini bulun: y"=e^(x^2-6x+5)*(2*x +6).

2) Belirli bir y"(1)=8*e^0=8 noktasında fonksiyonun değerini hesaplayın

Konuyla ilgili video

Yararlı tavsiye

Temel türevler tablosunu öğrenin. Bu önemli ölçüde zaman kazandıracaktır.

Kaynaklar:

• bir sabitin türevi

Peki irrasyonel bir denklem ile rasyonel bir denklem arasındaki fark nedir? Bilinmeyen değişken işaretin altındaysa kare kök ise denklemin irrasyonel olduğu kabul edilir.

Talimatlar

Bu tür denklemleri çözmenin ana yöntemi her iki tarafı da oluşturma yöntemidir. denklemler bir kareye. Fakat. bu doğaldır, yapmanız gereken ilk şey tabeladan kurtulmaktır. Bu yöntem teknik olarak zor değildir ancak bazen sıkıntılara yol açabilmektedir. Örneğin denklem v(2x-5)=v(4x-7) şeklindedir. Her iki tarafın karesini alırsak 2x-5=4x-7 elde ederiz. Böyle bir denklemi çözmek zor değil; x=1. Ama 1 rakamı verilmeyecek denklemler. Neden? Denklemde x'in değeri yerine bir koyarsak sağ ve sol taraflarda anlamsız ifadeler yer alır. Bu değer karekök için geçerli değildir. Bu nedenle 1 yabancı bir köktür ve bu nedenle bu denklemin kökleri yoktur.

Yani irrasyonel bir denklem her iki tarafının karesi alma yöntemi kullanılarak çözülür. Denklemi çözdükten sonra yabancı kökleri kesmek gerekir. Bunu yapmak için bulunan kökleri orijinal denklemde değiştirin.

Başka bir tane düşünün.
2х+vх-3=0
Elbette bu denklem bir önceki denklemin aynısı kullanılarak çözülebilir. Bileşikleri Taşı denklemler Karekökü olmayan , sağ tarafa ve ardından kare alma yöntemini kullanın. Ortaya çıkan rasyonel denklemi ve köklerini çözer. Ama aynı zamanda daha zarif bir tane daha. Yeni bir değişken girin; vх=y. Buna göre 2y2+y-3=0 formunda bir denklem elde edeceksiniz. Yani olağan ikinci dereceden denklem. Köklerini bulun; y1=1 ve y2=-3/2. Sonra iki tanesini çöz denklemler vх=1; vх=-3/2. İkinci denklemin kökleri yoktur; birinciden x=1 olduğunu buluruz. Kökleri kontrol etmeyi unutmayın.

Kimlikleri çözmek oldukça basittir. Bunu yapmak için, belirlenen hedefe ulaşılıncaya kadar aynı dönüşümlerin gerçekleştirilmesi gerekir. Böylece basit aritmetik işlemler yardımıyla ortaya çıkan problem çözülecektir.

İhtiyacın olacak

• - kağıt;
• - dolma kalem.

Talimatlar

Bu tür dönüşümlerin en basiti cebirsel kısaltılmış çarpmalardır (toplamın karesi (fark), kareler farkı, toplam (fark), toplamın küpü (fark) gibi). Ayrıca çok sayıda var ve trigonometrik formüller Bunlar aslında aynı kimliklerdir.

Nitekim iki terimin toplamının karesi, birincinin karesi artı birincinin ikinciyle çarpımının iki katı ve artı ikincinin karesine eşittir, yani (a+b)^2= (a+) b)(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Her ikisini de basitleştirin

Çözümün genel ilkeleri

Belirli bir integralin ne olduğunu matematiksel analiz veya yüksek matematikle ilgili bir ders kitabından tekrarlayın. Bilindiği üzere çözüm kesin integral türevi bir integral veren bir fonksiyon var. Bu işlev antiderivatif denir. Bu prensibe dayanarak ana integraller inşa edilir.
İntegral formuna göre tablo integrallerinden hangisinin uyduğunu belirleyin bu durumda. Bunu hemen belirlemek her zaman mümkün olmuyor. Çoğu zaman tablo biçimi ancak integrandın basitleştirilmesi için yapılan birkaç dönüşümden sonra fark edilebilir hale gelir.

Değişken Değiştirme Yöntemi

İntegral fonksiyonu ise trigonometrik fonksiyon Argümanı bazı polinomlar içeren değişkeni değiştirme yöntemini kullanmayı deneyin. Bunu yapmak için integralin argümanındaki polinomu yeni bir değişkenle değiştirin. Yeni ve eski değişkenler arasındaki ilişkiye dayanarak entegrasyonun yeni sınırlarını belirleyin. Bu ifadenin türevini alarak yeni diferansiyeli bulun. Yani alacaksın yeni türönceki integralin herhangi bir tablodaki integrale yakın veya hatta karşılık gelen.

İkinci Tür İntegrallerin Çözülmesi

İntegral ikinci türden bir integral ise, vektör görünümüİntegral fonksiyonunu kullanıyorsanız, bu integrallerden skaler integrallere geçiş için kuralları kullanmanız gerekecektir. Böyle bir kural Ostrogradsky-Gauss ilişkisidir. Bu yasa, belirli bir vektör fonksiyonunun rotor akısından, belirli bir vektör alanının diverjansı üzerinden üçlü integrale geçmemizi sağlar.

Entegrasyon sınırlarının değiştirilmesi

Antiderivatifi bulduktan sonra integralin limitlerini yerine koymak gerekir. İlk olarak, üst limitin değerini ters türev ifadesinde değiştirin. Bir numara alacaksınız. Daha sonra, elde edilen sayıdan alt limitten elde edilen başka bir sayıyı antiderivatife çıkarın. İntegralin limitlerinden biri sonsuzluk ise, bunu antiderivatif fonksiyona yerleştirirken limite gitmek ve ifadenin neye yöneldiğini bulmak gerekir.
İntegral iki boyutlu veya üç boyutlu ise, integralin nasıl değerlendirileceğini anlamak için integralin sınırlarını geometrik olarak temsil etmeniz gerekecektir. Aslında, örneğin üç boyutlu bir integral durumunda, integralin sınırları, entegre edilen hacmi sınırlayan tüm düzlemler olabilir.

Tanımından çıkar. Ve böylece sayının logaritması B dayalı A bir sayının yükseltilmesi gereken üs olarak tanımlanır A numarayı almak için B(logaritma yalnızca pozitif sayılar için mevcuttur).

Bu formülasyondan, hesaplama şu şekildedir: x=log a b, denklemi çözmeye eşdeğerdir a x =b.Örneğin, günlük 2 8 = 3Çünkü 8 = 2 3 . Logaritmanın formülasyonu şunu doğrulamayı mümkün kılar: b=a c, sonra sayının logaritması B dayalı A eşittir İle. Logaritma konusunun bir sayının kuvvetleri konusuyla yakından ilgili olduğu da açıktır.

Herhangi bir sayıda olduğu gibi logaritmalarla da şunları yapabilirsiniz: toplama, çıkarma işlemleri ve mümkün olan her şekilde dönüştürün. Ancak logaritmalar tamamen sıradan sayılar olmadığı için burada kendi özel kuralları geçerlidir. ana özellikler.

Logaritmaların toplanması ve çıkarılması.

Aynı tabanlara sahip iki logaritmayı alalım: x'i günlüğe kaydet Ve bir y'yi günlüğe kaydet. Daha sonra toplama ve çıkarma işlemlerini gerçekleştirmek mümkündür:

log a x+ log a y= log a (x·y);

log a x - log a y = log a (x:y).

bir günlüğe kaydet(X 1 . X 2 . X 3 ... xk) = x'i günlüğe kaydet 1 + x'i günlüğe kaydet 2 + x'i günlüğe kaydet 3 + ... + a x k'yi günlüğe kaydet.

İtibaren logaritma bölüm teoremi Logaritmanın bir özelliği daha elde edilebilir. Günlüğe kaydetmenin yaygın bir bilgi olduğu A 1= 0, dolayısıyla

kayıt A 1 /B=günlük A 1 - günlük bir b= -günlük bir b.

Bu, bir eşitliğin olduğu anlamına gelir:

log a 1 / b = - log a b.

Karşılıklı iki sayının logaritması aynı nedenden ötürü birbirinden yalnızca işaret bakımından farklılık gösterecektir. Bu yüzden:

Günlük 3 9= - günlük 3 1 / 9; log 5 1 / 125 = -log 5 125.

Bir sayının logaritması N dayalı A üs denir X oluşturmanız gereken A numarayı almak için N

Şartıyla
,
,

Logaritmanın tanımından şu sonuç çıkıyor
, yani
- bu eşitlik temel logaritmik özdeşliktir.

10 tabanına göre logaritmalara ondalık logaritma denir. Yerine
yazmak
.

Tabana göre logaritmalar e doğal olarak adlandırılır ve belirlenir
.

Logaritmanın temel özellikleri.

Birin logaritması herhangi bir taban için sıfıra eşittir.

Ürünün logaritması, faktörlerin logaritmasının toplamına eşittir.

3) Bölümün logaritması logaritmaların farkına eşittir

Faktör
logaritmalardan tabana geçiş modülü denir A tabandaki logaritmalara B .

2-5 özelliklerini kullanarak, karmaşık bir ifadenin logaritmasını logaritmalar üzerinde yapılan basit aritmetik işlemlerin sonucuna indirgemek genellikle mümkündür.

Örneğin,

Bir logaritmanın bu tür dönüşümlerine logaritma denir. Logaritmanın tersi olan dönüşümlere potansiyasyon denir.

Bölüm 2. Yüksek matematiğin unsurları.

1. Sınırlar

Fonksiyonun sınırı
sonlu bir sayıdır A eğer xx 0 önceden belirlenmiş her biri için
öyle bir sayı var ki
en kısa sürede
, O
.

Limiti olan bir fonksiyon ondan sonsuz küçük bir miktarda farklılık gösterir:
, nerede- b.m.v., yani.
.

Örnek. İşlevi düşünün
.

Çabalarken
, işlev sen sıfıra doğru eğilim gösterir:

1.1. Limitlerle ilgili temel teoremler.

Sabit bir değerin limiti bu sabit değere eşittir

.

Sonlu sayıda fonksiyonun toplamının (farkının) limiti, bu fonksiyonların limitlerinin toplamına (farkına) eşittir.

Sonlu sayıda fonksiyonun çarpımının limiti, bu fonksiyonların limitlerinin çarpımına eşittir.

Paydanın limiti sıfır değilse, iki fonksiyonun bölümünün limiti, bu fonksiyonların limitlerinin bölümüne eşittir.

Harika Sınırlar

,
, Nerede

1.2. Limit Hesaplama Örnekleri

Ancak tüm limitler bu kadar kolay hesaplanmıyor. Çoğu zaman, limitin hesaplanması şu türden bir belirsizliğin ortaya çıkarılmasına indirgenir: veya .

.

2. Bir fonksiyonun türevi

Bir fonksiyonumuz olsun
, segmentte sürekli
.

Argüman biraz artış var
. Daha sonra fonksiyon bir artış alacaktır
.

Bağımsız değişken değeri fonksiyon değerine karşılık gelir
.

Bağımsız değişken değeri
fonksiyon değerine karşılık gelir.

Buradan, .

Bu oranın limitini bulalım.
. Eğer bu limit mevcutsa buna verilen fonksiyonun türevi denir.

Tanım 3 Verilen bir fonksiyonun türevi
argümanla argümanın artışı keyfi olarak sıfıra yaklaştığında, bir fonksiyonun artışının argümanın artışına oranının limiti denir.

Bir fonksiyonun türevi
aşağıdaki gibi belirlenebilir:

; ; ; .

Tanım 4Bir fonksiyonun türevini bulma işlemine denir farklılaşma.

2.1. Türevin mekanik anlamı.

Katı bir cismin ya da maddesel bir noktanın doğrusal hareketini düşünelim.

Zamanın bir noktasında izin ver hareket noktası
uzaktaydı başlangıç ​​pozisyonundan
.

Bir süre sonra
mesafe kat etti
. Davranış =- maddi bir noktanın ortalama hızı
. Bunu dikkate alarak bu oranın limitini bulalım.
.

Sonuç olarak, maddi bir noktanın anlık hareket hızının belirlenmesi, yolun zamana göre türevinin bulunmasına indirgenir.

2.2. Türevin geometrik değeri

Grafiksel olarak tanımlanmış bir fonksiyonumuz olsun
.

Pirinç. 1. Türevin geometrik anlamı

Eğer
, sonra işaret et
, noktaya yaklaşarak eğri boyunca hareket edecek
.

Buradan
, yani argümanın belirli bir değeri için türevin değeri Belirli bir noktada tanjantın eksenin pozitif yönü ile oluşturduğu açının tanjantına sayısal olarak eşittir
.

2.3. Temel farklılaşma formülleri tablosu.

Güç fonksiyonu

Üstel fonksiyon

Logaritmik fonksiyon

Trigonometrik fonksiyon

Ters trigonometrik fonksiyon

2.4. Farklılaşma kuralları.

Türevi

Fonksiyonların toplamının (farkının) türevi

İki fonksiyonun çarpımının türevi

İki fonksiyonun bölümünün türevi

2.5. Türevi karmaşık fonksiyon.

Fonksiyon verilsin
şeklinde temsil edilebilecek şekilde

Ve
değişken burada o zaman bir ara argümandır

Karmaşık bir fonksiyonun türevi, verilen fonksiyonun ara argümana göre türevi ile ara argümanın x'e göre türevinin çarpımına eşittir.

Örnek 1.

Örnek 2.

3. Diferansiyel fonksiyon.

Olsun
, belirli bir aralıkta türevlenebilir
bırak gitsin en bu fonksiyonun bir türevi var

,

o zaman yazabiliriz

(1),

Nerede - sonsuz küçük bir miktar,

ne zamandan beri

Tüm eşitlik koşullarını (1) ile çarpmak
sahibiz:

Nerede
- b.m.v. yüksek mertebeden.

Büyüklük
fonksiyonun diferansiyeli denir
ve belirlenmiş

.

3.1. Diferansiyelin geometrik değeri.

Fonksiyon verilsin
.

İncir. 2. Diferansiyelin geometrik anlamı.

.

Açıkçası, fonksiyonun diferansiyeli
belirli bir noktadaki teğetin koordinatındaki artışa eşittir.

3.2. Çeşitli mertebelerden türevler ve diferansiyeller.

eğer oradaysa
, Daha sonra
birinci türev denir.

Birinci türevin türevine ikinci dereceden türev denir ve şöyle yazılır:
.

Fonksiyonun n'inci dereceden türevi
(n-1)'inci dereceden türev olarak adlandırılır ve şöyle yazılır:

.

Bir fonksiyonun diferansiyelinin diferansiyeline ikinci diferansiyel veya ikinci derece diferansiyel denir.

.

.

3.3 Biyolojik problemlerin farklılaşmayı kullanarak çözülmesi.

Görev 1. Çalışmalar, bir mikroorganizma kolonisinin büyümesinin yasalara uygun olduğunu göstermiştir.
, Nerede N – mikroorganizmaların sayısı (bin olarak), T – zaman (günler).

b) Bu dönemde koloninin nüfusu artacak mı yoksa azalacak mı?

Cevap. Koloninin boyutu artacaktır.

Görev 2. Göldeki su, patojen bakterilerin içeriğini izlemek için periyodik olarak test edilir. Başından sonuna kadar T testten sonraki günler, bakteri konsantrasyonu orana göre belirlenir

.

Gölde ne zaman minimum bakteri konsantrasyonu olacak ve içinde yüzmek mümkün olacak mı?

Çözüm: Bir fonksiyon, türevi sıfır olduğunda maksimum veya minimuma ulaşır.

,

Maksimum veya minimumun 6 gün sonra olacağını belirleyelim. Bunu yapmak için ikinci türevi alalım.

Cevap: 6 gün sonra minimum bakteri konsantrasyonu olacaktır.

logaritmanın tanımı

b'nin a tabanına göre logaritması, b'yi elde etmek için a'nın yükseltilmesi gereken üstür.

e numarası matematikte bir ifadenin ulaşmaya çalıştığı sınırı belirtmek gelenekseldir

e numarası dır-dir irrasyonel sayı - Bir ile ölçülemeyen bir sayı, ne tam sayı ne de kesir olarak doğru bir şekilde ifade edilemez. akılcı sayı.

Mektup e- Latince bir kelimenin ilk harfi ifade- gösteriş yapmak, dolayısıyla matematikteki adı üstel- üstel fonksiyon.

Sayı e matematikte ve şu ya da bu şekilde matematiksel hesaplamaları kendi ihtiyaçları için kullanan tüm bilimlerde yaygın olarak kullanılmaktadır.

Logaritmalar. Logaritmanın özellikleri

Tanım: Pozitif bir b sayısının tabanına göre logaritması, b sayısını elde etmek için a sayısının yükseltilmesi gereken c üssüdür.

Temel logaritmik kimlik:

7) Yeni bir üsse geçmenin formülü:

lna = log e a, e ≈ 2,718…

Logaritmalar konusundaki problemler ve testler. Logaritmanın özellikleri"

• Logaritmalar - Önemli Konular matematikte Birleşik Devlet Sınavını tekrarlamak için

Bu konudaki görevleri başarıyla tamamlamak için logaritmanın tanımını, logaritmanın özelliklerini, temel logaritmik özdeşliği, ondalık ve doğal logaritmanın tanımlarını bilmeniz gerekir. Bu konudaki ana problem türleri logaritmik ifadelerin hesaplanmasını ve dönüştürülmesini içeren problemlerdir. Aşağıdaki örnekleri kullanarak çözümlerini ele alalım.

Çözüm: Logaritmanın özelliklerini kullanarak şunu elde ederiz:

Çözüm: Derecelerin özelliklerini kullanarak şunu elde ederiz:

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Logaritmanın özellikleri, formülasyonları ve ispatları.

Logaritmaların bir takım özellikleri vardır karakteristik özellikler. Bu yazıda ana konulara bakacağız. logaritmanın özellikleri. Burada bunların formülasyonlarını vereceğiz, logaritmanın özelliklerini formül biçiminde yazacağız, uygulama örneklerini göstereceğiz ve ayrıca logaritmanın özelliklerinin kanıtını sunacağız.

Sayfada gezinme.

Logaritmanın temel özellikleri, formüller

Hatırlama ve kullanma kolaylığı için hayal edelim logaritmanın temel özellikleri formüllerin bir listesi şeklinde. Bir sonraki paragrafta bunların formülasyonlarını, kanıtlarını, kullanım örneklerini ve gerekli açıklamaları vereceğiz.

Birlik logaritmasının özelliği: herhangi bir a>0, a≠1 için log a 1=0.

Tabana eşit bir sayının logaritması: a>0, a≠1 için log a a=1.

Tabanın kuvvetinin logaritmasının özelliği: log a a p =p, burada a>0, a≠1 ve p herhangi bir gerçek sayıdır.

İki pozitif sayının çarpımının logaritması: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
ve n pozitif sayının çarpımının logaritmasının özelliği: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Bir bölümün logaritmasının özelliği: , burada a>0, a≠1, x>0, y>0.

Bir sayının kuvvetinin logaritması: log a b p =p·log a |b| burada a>0, a≠1, b ve p, b p derecesi anlamlı ve b p >0 olacak şekilde sayılardır.

Sonuçlar: , burada a>0, a≠1, n – doğal sayı, birden büyük, b>0.

Sonuç 1: , a>0 , a≠1 , b>0 , b≠1 .

Sonuç 2: , a>0 , a≠1 , b>0 , p ve q gerçek sayılardır, q≠0 , özellikle b=a için elimizde .

Formülasyonlar ve özelliklerin kanıtları

Logaritmanın yazılı özelliklerinin formülasyonuna ve ispatına geçiyoruz. Logaritmanın tüm özellikleri, logaritmanın tanımına ve ondan çıkan temel logaritmik özdeşliğe ve derecenin özelliklerine dayanarak kanıtlanmıştır.

İle başlayalım bir logaritmasının özellikleri. Formülasyonu şu şekildedir: Birliğin logaritması sıfıra eşittir, yani, 1=0'ı günlüğe kaydet herhangi bir a>0 için a≠1. Kanıt zor değildir: Yukarıdaki a>0 ve a≠1 koşullarını karşılayan herhangi bir a için a 0 =1 olduğundan, kanıtlanacak log a 1=0 eşitliği logaritmanın tanımından hemen çıkar.

Dikkate alınan özelliğin uygulamasına örnekler verelim: log 3 1=0, log1=0 ve .

Bir sonraki özelliğe geçelim: tabanına eşit bir sayının logaritması bire eşittir, yani, log a=1 a>0 için a≠1. Aslında, herhangi bir a için a 1 =a olduğundan, logaritmanın tanımı gereği log a a=1 olur.

Logaritmaların bu özelliğini kullanma örnekleri log 5 5=1, log 5,6 5,6 ve lne=1 eşitlikleridir.

Logaritmanın tabanına eşit bir sayının üssünün logaritması üssüne eşittir. Logaritmanın bu özelliği şu formdaki bir formüle karşılık gelir: log a a p =p, burada a>0, a≠1 ve p – herhangi bir gerçek sayı. Bu özellik doğrudan logaritmanın tanımından kaynaklanmaktadır. Logaritmanın değerini hemen belirtmenize izin verdiğini unutmayın, eğer logaritma işaretinin altındaki sayıyı tabanın kuvveti olarak temsil etmek mümkünse; logaritmayı hesaplama makalesinde bunun hakkında daha fazla konuşacağız.

Örneğin, log 2 2 7 =7, log10 -4 =-4 ve .

İki pozitif sayının çarpımının logaritması x ve y bu sayıların logaritmasının çarpımına eşittir: log a (x y)=log a x+log a y, a>0 , a≠1 . Bir çarpımın logaritmasının özelliğini kanıtlayalım. Derecenin özelliklerinden dolayı a log a x+log a y =a log a x ·a log a y ve ana logaritmik özdeşliğe göre a log a x =x ve a log a y =y olduğundan, a log a x ·a log a y =x·y. Böylece, logaritmanın tanımına göre eşitliğin kanıtlandığı log a x+log a y =x·y olur.

Bir çarpımın logaritması özelliğinin kullanımına ilişkin örnekler gösterelim: log 5 (2 3)=log 5 2+log 5 3 ve .

Bir çarpımın logaritmasının özelliği, x 1 , x 2 , …, x n pozitif sayılarından oluşan sonlu bir n sayısının çarpımına şu şekilde genelleştirilebilir: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Bu eşitlik matematiksel tümevarım yöntemi kullanılarak sorunsuz bir şekilde kanıtlanabilir.

Örneğin, çarpımın doğal logaritması 4, e ve sayılarının üç doğal logaritmasının toplamı ile değiştirilebilir.

İki pozitif sayının bölümünün logaritması x ve y bu sayıların logaritmaları arasındaki farka eşittir. Bir bölümün logaritmasının özelliği, formun formülüne karşılık gelir a>0, a≠1, x ve y bazı pozitif sayılardır. Bu formülün geçerliliği, bir çarpımın logaritması formülünün yanı sıra kanıtlanmıştır: çünkü , o zaman logaritmanın tanımı gereği .

Logaritmanın bu özelliğini kullanmanın bir örneği: .

Konusuna geçelim kuvvetin logaritmasının özelliği. Bir derecenin logaritması, üssün çarpımına ve bu derecenin tabanının modülünün logaritmasına eşittir. Bir kuvvetin logaritmasının bu özelliğini formül olarak yazalım: log a b p =p·log a |b| burada a>0, a≠1, b ve p, b p derecesi anlamlı ve b p >0 olacak şekilde sayılardır.

Öncelikle bu özelliği pozitif b için kanıtlayalım. Temel logaritmik özdeşlik, b sayısını a log a b, ardından b p =(a log a b) p olarak temsil etmemize olanak tanır ve ortaya çıkan ifade, kuvvet özelliği nedeniyle a p·log a b'ye eşittir. Böylece b p =a p·log a b eşitliğine ulaşıyoruz ve bundan logaritmanın tanımına göre log a b p =p·log a b sonucunu çıkarıyoruz.

Geriye bu özelliği negatif b için kanıtlamak kalıyor. Burada negatif b için log a b p ifadesinin yalnızca çift p üsleri için anlamlı olduğunu görüyoruz (çünkü b p derecesinin değeri sıfırdan büyük olmalıdır, aksi takdirde logaritmanın bir anlamı olmayacaktır) ve bu durumda b p =|b| P. O zaman b p =|b| p =(a log a |b|) p =a p·log a |b| , buradan log a b p =p·log a |b| .

Örneğin, ve ln(-3) 4 =4·ln|-3|=4·ln3 .

Önceki mülkten kaynaklanmaktadır kökten logaritmanın özelliği: n'inci kökün logaritması, 1/n kesrinin radikal ifadenin logaritmasına göre çarpımına eşittir, yani a>0, a≠1, n birden büyük bir doğal sayıdır, b>0 .

Kanıt, herhangi bir pozitif b için geçerli olan eşitliğe (kesirli üslü üs tanımına bakınız) ve üssün logaritmasının özelliğine dayanmaktadır: .

Bu özelliği kullanmanın bir örneğini burada bulabilirsiniz: .

Şimdi kanıtlayalım yeni bir logaritma tabanına geçme formülü tip . Bunu yapmak için log c b=log a blog·log c a eşitliğinin geçerliliğini kanıtlamak yeterlidir. Temel logaritmik kimlik, b sayısını a log a b olarak temsil etmemize ve ardından log c b=log ca log a b olarak göstermemize olanak tanır. Geriye derecenin logaritması özelliğini kullanmak kalır: log c a log a b =log a b·log ca . Bu, log c b=log a b·log c a eşitliğini kanıtlar; bu, logaritmanın yeni tabanına geçiş formülünün de kanıtlanmış olduğu anlamına gelir .

Logaritmanın bu özelliğini kullanmaya ilişkin birkaç örnek gösterelim: ve .

Yeni bir tabana geçme formülü, "uygun" bir tabana sahip logaritmalarla çalışmaya devam etmenize olanak tanır. Örneğin, bir logaritma tablosundan bir logaritmanın değerini hesaplayabilmeniz için doğal veya ondalık logaritmalara geçmek için kullanılabilir. Yeni bir logaritma tabanına geçme formülü, bazı durumlarda, bazı logaritmaların diğer tabanlarla değerleri bilindiğinde belirli bir logaritmanın değerini bulmayı da sağlar.

Sıklıkla kullanılır özel durum formun c=b olduğu yeni bir logaritma tabanına geçiş formülleri. Bu, log a b ve log b a'nın karşılıklı olarak ters sayılar olduğunu gösterir. Örneğin, .

Logaritmanın değerlerini bulmak için uygun olan formül de sıklıkla kullanılır. Sözlerimizi doğrulamak için formun logaritmasının değerini hesaplamak için nasıl kullanılabileceğini göstereceğiz. Sahibiz . Formülü kanıtlamak için, logaritmanın yeni bir tabanına geçmek için formülü kullanmak yeterlidir: .

Logaritmaların karşılaştırılması özelliklerini kanıtlamak için kalır.

Tam tersi yöntemi kullanalım. a 1 >1, a 2 >1 ve a 1 2 ve 0 1 için log a 1 b≤log a 2 b'nin doğru olduğunu varsayalım. Logaritmanın özelliklerine dayanarak bu eşitsizlikler şu şekilde yeniden yazılabilir: Ve sırasıyla log b a 1 ≤log b a 2 ve log b a 1 ≥log b a 2 olur. O halde aynı tabanlara sahip kuvvetlerin özelliklerine göre b log b a 1 ≥b log b a 2 ve b log b a 1 ≥b log b a 2 eşitlikleri geçerli olmalıdır, yani a 1 ≥a 2 . Böylece a 1 2 koşuluyla bir çelişkiye geldik. Bu ispatı tamamlar.

Logaritmanın temel özellikleri

• Ders için materyaller
• Tüm formülleri indir

Logaritmalar da diğer sayılar gibi her şekilde toplanabilir, çıkarılabilir ve dönüştürülebilir. Ancak logaritmalar tam olarak sıradan sayılar olmadığından burada kurallar vardır. ana özellikler.

Bu kuralları kesinlikle bilmeniz gerekir; onlar olmadan tek bir ciddi logaritmik problem çözülemez. Ayrıca bunlardan çok azı var - her şeyi bir günde öğrenebilirsiniz. Öyleyse başlayalım.

Logaritmaların toplanması ve çıkarılması

Aynı tabanlara sahip iki logaritmayı düşünün: log a x ve log a y. Daha sonra bunlar eklenebilir ve çıkarılabilir ve:

Yani logaritmaların toplamı çarpımın logaritmasına, fark ise bölümün logaritmasına eşittir. Lütfen dikkat: buradaki kilit nokta aynı gerekçeler. Sebepler farklıysa bu kurallar işe yaramaz!

Bu formüller, tek tek parçaları dikkate alınmasa bile logaritmik bir ifadeyi hesaplamanıza yardımcı olacaktır (“Logaritma nedir” dersine bakın). Örneklere bir göz atın ve şunu görün:

Görev. İfadenin değerini bulun: log 6 4 + log 6 9.

Logaritmaların tabanları aynı olduğundan toplam formülünü kullanırız:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Görev. İfadenin değerini bulun: log 2 48 – log 2 3.

Bazlar aynı, fark formülünü kullanıyoruz:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Görev. İfadenin değerini bulun: log 3 135 – log 3 5.

Tabanlar yine aynı olduğundan elimizde:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Gördüğünüz gibi orijinal ifadeler ayrı olarak hesaplanmayan “kötü” logaritmalardan oluşuyor. Ancak dönüşümlerden sonra tamamen normal sayılar elde edilir. Birçok test bu gerçeğe dayanmaktadır. Evet, Birleşik Devlet Sınavında test benzeri ifadeler tüm ciddiyetiyle (bazen neredeyse hiç değişiklik yapılmadan) sunulmaktadır.

Üslü logaritmadan çıkarma

Şimdi görevi biraz karmaşıklaştıralım. Ya bir logaritmanın tabanı veya argümanı bir kuvvet ise? Daha sonra bu derecenin üssü aşağıdaki kurallara göre logaritmanın işaretinden çıkarılabilir:

• log a x n = n · log a x ;
• 
• 

Son kuralın ilk ikisini takip ettiğini görmek kolaydır. Ancak yine de hatırlamak daha iyidir - bazı durumlarda hesaplama miktarını önemli ölçüde azaltacaktır.

Elbette, logaritmanın ODZ'sine uyulursa tüm bu kurallar anlamlıdır: a > 0, a ≠ 1, x > 0. Ve bir şey daha: tüm formülleri yalnızca soldan sağa değil, aynı zamanda tam tersi şekilde uygulamayı öğrenin. , yani Logaritma işaretinden önceki sayıları logaritmanın kendisine girebilirsiniz. En sık ihtiyaç duyulan şey budur.

Görev. İfadenin değerini bulun: log 7 49 6 .

İlk formülü kullanarak argümandaki dereceden kurtulalım:
günlük 7 49 6 = 6 günlük 7 49 = 6 2 = 12

Görev. İfadenin anlamını bulun:

[Resmin başlığı]

Paydanın, tabanı ve argümanının tam kuvvetleri olan bir logaritma içerdiğine dikkat edin: 16 = 2 4; 49 = 7 2. Sahibiz:

[Resmin başlığı]

Son örneğin biraz açıklama gerektirdiğini düşünüyorum. Logaritmalar nereye gitti? Son ana kadar sadece paydayla çalışıyoruz. Orada duran logaritmanın temelini ve argümanını kuvvetler şeklinde sunduk ve üsleri çıkardık - “üç katlı” bir kesir elde ettik.

Şimdi ana kesirlere bakalım. Pay ve payda aynı sayıyı içerir: log 2 7. Log 2 7 ≠ 0 olduğundan kesri azaltabiliriz - 2/4 paydada kalacaktır. Aritmetik kurallarına göre dörtlü paya aktarılabilir ki yapılan da budur. Sonuç şuydu: 2.

Yeni bir temele geçiş

Logaritma toplama ve çıkarma kurallarından bahsederken bunların sadece aynı tabanlarla çalıştığını özellikle vurguladım. Peki ya sebepler farklıysa? Ya aynı sayının tam kuvvetleri değilse?

Yeni bir vakfa geçiş formülleri kurtarmaya geliyor. Bunları bir teorem şeklinde formüle edelim:

Logaritma log a x verilsin. O halde c > 0 ve c ≠ 1 olacak şekilde herhangi bir c sayısı için eşitlik doğrudur:

[Resmin başlığı]

Özellikle c = x değerini ayarlarsak şunu elde ederiz:

[Resmin başlığı]

İkinci formülden, logaritmanın tabanının ve argümanının değiştirilebileceği anlaşılmaktadır, ancak bu durumda ifadenin tamamı "tersine çevrilmiştir", yani. logaritma paydada görünür.

Bu formüllere sıradan sayısal ifadelerde nadiren rastlanır. Ne kadar kullanışlı olduklarını ancak logaritmik denklem ve eşitsizlikleri çözerken değerlendirmek mümkündür.

Ancak yeni bir temele taşınmak dışında hiçbir şekilde çözülemeyen sorunlar var. Bunlardan birkaçına bakalım:

Görev. İfadenin değerini bulun: log 5 16 log 2 25.

Her iki logaritmanın argümanlarının tam güçler içerdiğini unutmayın. Göstergeleri çıkaralım: log 5 16 = log 5 2 4 = 4log 5 2; günlük 2 25 = günlük 2 5 2 = 2 günlük 2 5;

Şimdi ikinci logaritmayı “tersine çevirelim”:

[Resmin başlığı]

Faktörleri yeniden düzenlerken çarpım değişmediğinden, sakince dört ve ikiyi çarptık ve ardından logaritmalarla uğraştık.

Görev. İfadenin değerini bulun: log 9 100 lg 3.

Birinci logaritmanın tabanı ve argümanı tam kuvvetlerdir. Bunu bir kenara yazalım ve göstergelerden kurtulalım:

[Resmin başlığı]

Şimdi yeni bir tabana geçerek ondalık logaritmadan kurtulalım:

[Resmin başlığı]

Temel logaritmik kimlik

Çoğu zaman çözüm sürecinde bir sayının belirli bir tabana göre logaritması olarak gösterilmesi gerekir. Bu durumda aşağıdaki formüller bize yardımcı olacaktır:

1. n = log a a n

2. İlk durumda, n sayısı argümandaki üs haline gelir. N sayısı kesinlikle herhangi bir şey olabilir çünkü bu yalnızca bir logaritma değeridir.

   İkinci formül aslında başka kelimelerle ifade edilmiş bir tanımdır. Buna denir: temel logaritmik özdeşlik.

   Aslında b sayısı, b sayısının bu kuvveti a sayısını verecek şekilde yükseltilirse ne olur? Doğru: sonuç aynı a sayısıdır. Bu paragrafı dikkatlice tekrar okuyun; birçok kişi buna takılıp kalıyor.

   Yeni bir tabana geçiş formülleri gibi, temel logaritmik özdeşlik de bazen mümkün olan tek çözümdür.

   [Resmin başlığı]

   Log 25 64 = log 5 8 olduğuna dikkat edin - basitçe logaritmanın tabanından ve argümanından kareyi aldık. Aynı tabanla kuvvetleri çarpma kurallarını hesaba katarsak şunu elde ederiz:

   [Resmin başlığı]

   Bilmeyen varsa, bu Birleşik Devlet Sınavından gerçek bir görevdi :)

   Logaritmik birim ve logaritmik sıfır

   Sonuç olarak, özellik olarak adlandırılması pek mümkün olmayan iki kimlik vereceğim - bunlar daha ziyade logaritmanın tanımının sonuçlarıdır. Sürekli olarak sorunlarla karşılaşıyorlar ve şaşırtıcı bir şekilde "ileri düzey" öğrenciler için bile sorunlar yaratıyorlar.

   1. log a a = 1 logaritmik bir birimdir. Bir kere şunu unutmayın: o tabanın herhangi bir a tabanının logaritması bire eşittir.
   2. log a 1 = 0 logaritmik sıfırdır. A tabanı herhangi bir şey olabilir, ancak argüman bir içeriyorsa logaritma sıfıra eşittir! Çünkü 0 = 1, tanımın doğrudan bir sonucudur.

   Tüm özellikler bu kadar. Bunları uygulamaya koymayı unutmayın! Dersin başındaki kopya kağıdını indirin, yazdırın ve problemleri çözün.

   Logaritma. Logaritmanın özellikleri (toplama ve çıkarma).

   Logaritmanın özellikleri tanımından takip edin. Ve böylece sayının logaritması B dayalı A bir sayının yükseltilmesi gereken üs olarak tanımlanır A numarayı almak için B(logaritma yalnızca pozitif sayılar için mevcuttur).

   Bu formülasyondan, hesaplama şu şekildedir: x=log a b, denklemi çözmeye eşdeğerdir a x =b.Örneğin, günlük 2 8 = 3Çünkü 8 = 2 3 . Logaritmanın formülasyonu şunu doğrulamayı mümkün kılar: b=a c, sonra sayının logaritması B dayalı A eşittir İle. Logaritma konusunun kuvvetler konusuyla yakından ilişkili olduğu da açıktır.

   Herhangi bir sayıda olduğu gibi logaritmalarla da şunları yapabilirsiniz: toplama, çıkarma işlemleri ve mümkün olan her şekilde dönüştürün. Ancak logaritmalar tamamen sıradan sayılar olmadığı için burada kendi özel kuralları geçerlidir. ana özellikler.

   Logaritmaların toplanması ve çıkarılması.

   Aynı tabanlara sahip iki logaritmayı alalım: x'i günlüğe kaydet Ve bir y'yi günlüğe kaydet. Daha sonra toplama ve çıkarma işlemlerini gerçekleştirmek mümkündür:

   Gördüğümüz gibi, logaritmaların toplamıürünün logaritmasına eşittir ve fark logaritmalar- bölümün logaritması. Üstelik sayılar doğruysa bu doğrudur. A, X Ve en pozitif ve a ≠ 1.

   Bu formüllerdeki ana hususun aynı temeller olduğuna dikkat etmek önemlidir. Gerekçeler farklı ise bu kurallar geçerli değildir!

   Aynı tabanlara sahip logaritmaların eklenmesi ve çıkarılmasına ilişkin kurallar yalnızca soldan sağa değil, aynı zamanda tam tersi şekilde de okunur. Sonuç olarak, çarpımın logaritması ve bölümün logaritması için teoremlerimiz var.

   Ürünün logaritması iki pozitif sayı logaritmalarının toplamına eşittir ; bu teoremi yeniden ifade edersek aşağıdakileri elde ederiz: eğer sayılar A, X Ve en pozitif ve bir ≠ 1, O:

   Bölümün logaritması iki pozitif sayı, bölünenin logaritması ile bölenin logaritması arasındaki farka eşittir. Başka bir deyişle, sayılar A, X Ve en pozitif ve bir ≠ 1, O:

   Yukarıdaki teoremleri çözmek için uygulayalım. örnekler:

   Eğer sayılar X Ve en negatif o zaman çarpım logaritması formülü anlamsız hale gelir. Bu nedenle aşağıdakileri yazmak yasaktır:

   log 2 (-8) ve log 2 (-4) ifadeleri hiç tanımlı olmadığından (logaritmik fonksiyon) en= günlük 2 X yalnızca pozitif bağımsız değişken değerleri için tanımlanmış X).

   Ürün teoremi sadece iki faktör için değil aynı zamanda sınırsız sayıda faktör için de geçerlidir. Bu şu anlama gelir; her doğal k ve herhangi bir pozitif sayı X 1 , X 2 , . . . ,xn bir kimlik var:

   İtibaren logaritma bölüm teoremi Logaritmanın bir özelliği daha elde edilebilir. Günlüğe kaydetmenin yaygın bir bilgi olduğu A 1= 0, dolayısıyla

   Bu, bir eşitliğin olduğu anlamına gelir:

   Karşılıklı iki sayının logaritması aynı nedenden ötürü birbirinden yalnızca işaret bakımından farklılık gösterecektir. Bu yüzden:

   Logaritma. Logaritmanın özellikleri

   Logaritma. Logaritmanın özellikleri

   Eşitliği ele alalım. ve değerlerini bize bildirin ve değerini bulmak istiyoruz.

   Yani, elde etmek için kurmamız gereken üssü arıyoruz.

   İzin vermek Bir değişken herhangi bir gerçek değeri alabilirse, değişkenlere aşağıdaki kısıtlamalar uygulanır: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

   Ve değerlerini biliyorsak ve bilinmeyeni bulma göreviyle karşı karşıya kalırsak, bu amaçla adı verilen matematiksel bir işlem uygulanır. logaritma.

   Aldığımız değeri bulmak için bir sayının logaritmasıİle temel :

   Bir sayının tabanına göre logaritması, elde edilmesi için yükseltilmesi gereken üstür.

   Yani temel logaritmik kimlik:

   o» başlık=»a>o»/> , 1″ başlık=»a1″/>, 0″ başlık=»b>0″/>

   esasen matematiksel gösterim logaritmanın tanımları.

   Logaritmanın matematiksel işlemi üstel alma işleminin tersidir, dolayısıyla logaritmanın özellikleri derecenin özellikleriyle yakından ilişkilidir.

   Başlıcalarını listeleyelim logaritmanın özellikleri:

   (o" başlık='a>o"/> , 1″ başlık=»a1″/>, 0″ başlık=»b>0″/>, 0,

   d>0″/>, 1″ başlık=”d1″/>

   4.

   5.

   Aşağıdaki özellik grubu, bir ifadenin üssünü logaritmanın işareti altında temsil etmenize veya logaritmanın tabanında logaritmanın işaretinin önünde bir katsayı biçiminde durmanıza olanak tanır:

   6.

   7.

   8.

   9.

   Bir sonraki formül grubu, belirli bir tabana sahip bir logaritmadan keyfi bir tabana sahip bir logaritmaya geçmenizi sağlar ve denir yeni bir tabana geçiş formülleri:

   10.

   12. (özellik 11'in sonucu)

   

   Aşağıdaki üç özellik iyi bilinmemektedir, ancak logaritmik denklemleri çözerken veya logaritma içeren ifadeleri basitleştirirken sıklıkla kullanılırlar:

   13.

   14.

   15.

   Özel durumlar:

   — ondalık logaritma

   — doğal logaritma

   Logaritma içeren ifadeleri basitleştirirken genel bir yaklaşım kullanılır:

   1. Tanıtım ondalık sayılar sıradan olanlar şeklinde.

   2. Karışık sayılar uygunsuz kesirler olarak temsil edilir.

   3. Logaritmanın tabanındaki ve logaritmanın işareti altındaki sayıları basit faktörlere ayırıyoruz.

   4. Tüm logaritmaları aynı tabana indirmeye çalışıyoruz.

   5. Logaritmanın özelliklerini uygulayabilecektir.

   Logaritma içeren ifadeleri basitleştirme örneklerine bakalım.

   Örnek 1.

   Hesaplamak:

   Tüm üsleri basitleştirelim: Görevimiz onları, üssü üssüyle aynı sayı olan logaritmaya indirgemektir.

   ==(özellik 7'ye göre)=(özellik 6'ya göre) =

   Aldığımız göstergeleri orijinal ifadede yerine koyalım. Şunu elde ederiz:

   Cevap: 5.25

   Örnek 2. Hesaplayın:

   

   Tüm logaritmaları 6 tabanına indirelim (bu durumda kesrin paydasındaki logaritmalar paya "geçecektir"):

   Logaritma işaretinin altındaki sayıları basit faktörlere ayıralım:

   4 ve 6 numaralı özellikleri uygulayalım:

   Değiştirmeyi tanıtalım

   Şunu elde ederiz:

   Cevap 1

   Logaritma . Temel logaritmik özdeşlik.

   Logaritmanın özellikleri. Ondalık logaritma. Doğal logaritma.

   Logaritma pozitif sayı N'den tabana (B > 0, B 1) N elde etmek için b'nin yükseltilmesi gereken x üssü .

   Bu giriş aşağıdakine eşdeğerdir: b x = N .

   Örnekler: log 3 81 = 4, çünkü 3 4 = 81;

   günlük 1/3 27 = – 3, çünkü (1/3) - 3 = 3 3 = 27.

   Logaritmanın yukarıdaki tanımı bir özdeşlik olarak yazılabilir:

   

   Logaritmanın temel özellikleri.

   2) log 1 = 0, çünkü B 0 = 1 .

   3) Ürünün logaritması, faktörlerin logaritmasının toplamına eşittir:

   4) Bölümün logaritması, bölenin logaritması ile bölenin logaritması arasındaki farka eşittir:

   5) Bir kuvvetin logaritması üssün logaritması ile üssün çarpımına eşittir:

   Bu özelliğin sonucu şudur: kökün logaritması radikal sayının logaritmasının kökün kuvvetine bölünmesine eşittir:

   

   6) Logaritmanın tabanı bir derece ise, o zaman değer göstergenin tersi derece, günlük kafiye işaretinden çıkarılabilir:

   

   Son iki özellik tek bir özellikte birleştirilebilir:

   

   7) Geçiş modülü formülü (yani bir logaritma tabanından diğer tabana geçiş):

   

   Özel durumda ne zaman N=a sahibiz:

   

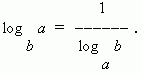
   Ondalık logaritma isminde taban logaritması 10. lg olarak belirlenmiştir, yani. günlük 10 N= günlük N. 10, 100, 1000, . p sırasıyla 1, 2, 3,…'dir, yani. o kadar çok olumlu şey var ki

   Birimler, logaritmik bir sayıda birden sonra kaç tane sıfır vardır? 0,1, 0,01, 0,001, . p sırasıyla –1, –2, –3,…, yani. logaritmik sayıdaki birden önceki sıfır sayısı kadar (sıfır tamsayılar dahil) negatif olan sayısı vardır. Diğer sayıların logaritmalarının kesirli kısmı vardır. mantis. Bütün parça logaritma denir karakteristik. Pratik kullanım için ondalık logaritmalar en uygunudur.

   Doğal logaritma isminde taban logaritması e. ln ile gösterilir, yani. kayıt e N= günlük N. Sayı e irrasyoneldir, yaklaşık değeri 2,718281828'dir. Sayının yöneldiği sınırdır (1 + 1 / N) N sınırsız artışla N(santimetre. ilk harika sınır"Limitler" sayfasında sayı dizileri»).
   Garip görünse de, fonksiyonların analizi ile ilgili çeşitli işlem türlerini gerçekleştirirken doğal logaritmaların çok kullanışlı olduğu ortaya çıktı. Tabana göre logaritmaların hesaplanması e diğer nedenlerden çok daha hızlı gerçekleştirilir.

• Rusya'da bir çocuğu evlat edinmek için bugün neye ihtiyaç var? Rusya'da evlat edinme, sorumlu kişisel kararın yanı sıra bir dizi prosedürü de içerir devlet denetimi adaylar. için zorlu seçim hazırlık aşaması daha fazlasına katkıda bulunur […]
• Rusya genelindeki vergi sicilinden TIN veya OGRN hakkında ücretsiz bilgi - çevrimiçi Birleşik Vergi Hizmetleri Portalında aşağıdakiler hakkında bilgi alabilirsiniz: devlet kaydı tüzel kişiler, bireysel girişimciler, […]
• Belgesiz araç kullanmanın cezası (ehliyet, sigorta, STS) Bazen unutkanlık nedeniyle sürücüler ehliyetsiz direksiyona geçiyor ve belgesiz araç kullanmanın cezasıyla karşılaşıyor. Bir otomobil tutkununun sahip olması gerektiğini hatırlatmak isteriz ki […]
• Erkekler için çiçekler. Bir erkeğe hangi çiçekler verilebilir? Bir erkeğe hangi çiçekler verilebilir? Çok fazla "erkek" çiçek yok ama erkeklere verilenler var. Önünüzde küçük bir çiçek listesi: Krizantemler. Güller. Karanfiller. […]
• Bir not özel biçimİşletmenin iç ortamında kullanılan ve mevcut üretim sorunlarının hızlı bir şekilde çözülmesine hizmet eden belge. Tipik olarak bu belge bazı şeyleri tanıtmak amacıyla hazırlanır […]
• Emekli maaşınızın finanse edilen kısmını Sberbank'tan ne zaman ve nasıl alacaksınız? Sberbank, devlet emeklilik fonunun ortak bankasıdır. Buna dayanarak, fonlu bir emekli maaşı için kayıt yaptıran vatandaşlar fonlanan kısmı transfer edebilir […]
• 2018'de Ulyanovsk ve Ulyanovsk bölgesinde çocuk yardımları Ayrıca tüm bölgelerde federal mevzuat tarafından onaylanan programlar faaliyet göstermektedir. Kimin hangi faydalara güvenebileceğine bakalım. Bölgesel yetkililer nasıl […]
• Detaylı Kılavuzçıkarları temsil etmek için vekaletname nasıl hazırlanır bireysel mahkemede Bir hukuk veya tahkim iddiasında, idari veya ceza davasında, hem davacının hem de davalının çıkarları bir avukat tarafından temsil edilebilir: […]