Wyznaczanie ciągłości funkcji w punkcie. Funkcja ciągła
Na tej lekcji nauczymy się wyznaczać ciągłość funkcji. Zrobimy to za pomocą limitów, do tego jednostronnych - prawego i lewego, które wcale nie są straszne, mimo że są zapisane jako i .
Ale czym w ogóle jest ciągłość funkcji? Dopóki nie dojdziemy do ścisłej definicji, najłatwiej wyobrazić sobie linię, którą można narysować bez odrywania ołówka od papieru. Jeśli taka linia zostanie narysowana, to jest ciągła. Linia ta jest wykresem funkcji ciągłej.
Graficznie funkcja jest ciągła w pewnym punkcie, jeśli jej wykres nie „załamuje się” w tym punkcie. Wykres takiej funkcji ciągłej to ![]() pokazano na poniższym rysunku.
pokazano na poniższym rysunku.

Wyznaczanie ciągłości funkcji poprzez granicę. Funkcja jest ciągła w punkcie, jeśli spełnione są trzy warunki:
1. Funkcja jest zdefiniowana w punkcie .
Jeżeli choć jeden z wymienionych warunków nie jest spełniony, to funkcja nie jest w punkcie ciągła. W tym przypadku mówią, że funkcja ma nieciągłość, a punkty na wykresie, w których wykres jest przerwany, nazywane są punktami nieciągłości funkcji. Wykres takiej funkcji, która wykazuje nieciągłość w punkcie x=2 przedstawiono na rysunku poniżej.

Przykład 1. Funkcjonować F(X) definiuje się następująco:

Czy ta funkcja będzie ciągła w każdym z punktów granicznych jej gałęzi, czyli w punktach X = 0 , X = 1 , X = 3 ?
Rozwiązanie. Sprawdzamy wszystkie trzy warunki ciągłości funkcji w każdym punkcie granicznym. Pierwszy warunek jest spełniony, od czego zdefiniowana funkcja w każdym z punktów granicznych wynika z definicji funkcji. Pozostaje sprawdzić pozostałe dwa warunki.
Kropka X= 0 . Znajdźmy lewą granicę w tym punkcie:
![]() .
.
Znajdźmy granicę po prawej stronie:
X Należy znaleźć = 0 dla tej gałęzi funkcji, która zawiera ten punkt, czyli drugiej gałęzi. Znajdujemy je:
Jak widać granica funkcji i wartość funkcji w punkcie X= 0 są równe. Zatem funkcja jest ciągła w tym punkcie X = 0 .
Kropka X= 1 . Znajdźmy lewą granicę w tym punkcie:
Znajdźmy granicę po prawej stronie:

Granica funkcji i wartość funkcji w punkcie X= 1 należy znaleźć dla tej gałęzi funkcji, która zawiera ten punkt, czyli drugiej gałęzi. Znajdujemy je:
 .
.
Granica funkcji i wartość funkcji w punkcie X= 1 są równe. Zatem funkcja jest ciągła w tym punkcie X = 1 .
Kropka X= 3 . Znajdźmy lewą granicę w tym punkcie:
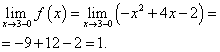
Znajdźmy granicę po prawej stronie:

Granica funkcji i wartość funkcji w punkcie X= 3 należy znaleźć dla tej gałęzi funkcji, która zawiera ten punkt, czyli drugiej gałęzi. Znajdujemy je:
 .
.
Granica funkcji i wartość funkcji w punkcie X= 3 są równe. Zatem funkcja jest ciągła w tym punkcie X = 3 .
Główny wniosek: funkcja ta jest ciągła w każdym punkcie granicznym.
Ustal samodzielnie ciągłość funkcji w pewnym punkcie, a następnie przyjrzyj się rozwiązaniu
Ciągłą zmianę funkcji można zdefiniować jako zmianę stopniową, bez skoków, w której niewielka zmiana argumentu pociąga za sobą małą zmianę funkcji.
Zilustrujmy tę ciągłą zmianę funkcji przykładem.

Niech ciężar zawiśnie na nitce nad stołem. Pod wpływem tego obciążenia nić rozciąga się, a więc i odległość l obciążenie od punktu zawieszenia gwintu jest funkcją masy obciążenia M, to jest l = F(M) , M≥0 .
Jeśli nieznacznie zmienisz masę ładunku, to odległość l zmieni się niewiele: małe zmiany M małe zmiany odpowiadają l. Jeśli jednak masa obciążenia jest bliska wytrzymałości nici na rozciąganie, wówczas niewielki wzrost masy obciążenia może spowodować zerwanie gwintu: odległość l wzrośnie gwałtownie i zrówna się z odległością punktu zawieszenia od powierzchni stołu. Wykres funkcji l = F(M) pokazany na rysunku. Na pewnym odcinku wykres ten jest linią ciągłą (ciągłą), a w pewnym momencie jest przerywany. Rezultatem jest graf składający się z dwóch gałęzi. We wszystkich punktach z wyjątkiem funkcji l = F(M) jest ciągły, ale w pewnym momencie ma nieciągłość.
Badanie funkcji pod kątem ciągłości może być samodzielnym zadaniem lub jednym z etapów pełnego badania funkcji i konstruowania jej wykresu.
Ciągłość funkcji na przedziale
Niech funkcja y = F(X) zdefiniowany w przedziale ] A, B[ i jest ciągły w każdym punkcie tego przedziału. Wtedy nazywa się to ciągłym w przedziale] A, B[ . Podobnie definiuje się pojęcie ciągłości funkcji na przedziałach postaci ]- ∞, B[ , ]A, + ∞[, ]- ∞, + ∞[. Niech teraz funkcja y = F(X) zdefiniowany na przedziale [ A, B] . Różnica między przedziałem a odcinkiem: punkty graniczne przedziału nie są uwzględniane w przedziale, ale punkty graniczne odcinka są uwzględniane w segmencie. W tym miejscu należy wspomnieć o tzw. ciągłości jednostronnej: w punkcie A, pozostając w segmencie [ A, B] , możemy podejść tylko od prawej strony i do rzeczy B- tylko po lewej stronie. Mówi się, że funkcja jest ciągła na przedziale [ A, B] , jeśli jest ciągły we wszystkich wewnętrznych punktach tego odcinka, ciągły po prawej stronie w tym punkcie A i pozostaje ciągła w tym punkcie B.
Przykładem funkcji ciągłej może być dowolna z funkcji elementarnych. Każda funkcja elementarna jest ciągła w dowolnym przedziale, w którym jest zdefiniowana. Na przykład funkcje i są ciągłe w dowolnym przedziale [ A, B], funkcja jest ciągła na przedziale [ 0 , B] , funkcja jest ciągła na dowolnym odcinku niezawierającym punktu A = 2 .
Przykład 4. Zbadaj ciągłość funkcji.
Rozwiązanie. Sprawdźmy pierwszy warunek. Funkcja nie jest zdefiniowana w punktach - 3 i 3. Przynajmniej jeden z warunków ciągłości funkcji na całej osi liczbowej nie jest spełniony. Zatem funkcja ta jest ciągła na przedziałach
.Przykład 5. Określ, przy jakiej wartości parametru A ciągły przez cały czas dziedzina definicji funkcjonować 
Rozwiązanie.
Znajdźmy prawą granicę w:
![]() .
.
Oczywiście wartość w danym punkcie X= 2 powinno być równe topór :
![]()
A = 1,5 .
Przykład 6. Określ, przy jakich wartościach parametrów A I B ciągły przez cały czas dziedzina definicji funkcjonować 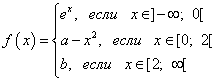
Rozwiązanie.
Znajdźmy lewą granicę funkcji w punkcie:
![]() .
.
Dlatego wartość w tym punkcie musi wynosić 1:
Znajdźmy funkcję po lewej stronie w punkcie:
Oczywiście wartość funkcji w punkcie powinna być równa:
Odpowiedź: funkcja jest ciągła w całym obszarze definicji, gdy A = 1; B = -3 .
Podstawowe własności funkcji ciągłych
Matematyka doszła do koncepcji funkcji ciągłej, badając przede wszystkim różne prawa ruchu. Przestrzeń i czas są nieskończone, a zależnością są na przykład ścieżki S od czasu T, wyrażone przez prawo S = F(T) , daje przykład ciągłego Funkcje F(T) . Temperatura podgrzanej wody również zmienia się w sposób ciągły i jest także ciągłą funkcją czasu: T = F(T) .
W analizie matematycznej udowodniono niektóre właściwości funkcji ciągłych. Przedstawmy najważniejsze z tych właściwości.
1. Jeżeli funkcja ciągła na pewnym przedziale przyjmuje wartości różnych znaków na końcach przedziału, to w pewnym punkcie tego przedziału przyjmuje wartość równy zeru. W bardziej formalnym ujęciu właściwość ta jest podana w twierdzeniu znanym jako pierwsze twierdzenie Bolzano-Cauchy'ego.
2. Funkcja F(X) , ciągły na przedziale [ A, B], przyjmuje wszystkie wartości pośrednie pomiędzy wartościami w punktach końcowych, czyli pomiędzy F(A) I F(B) . W bardziej formalnym ujęciu właściwość ta jest podana w twierdzeniu znanym jako drugie twierdzenie Bolzano-Cauchy'ego.
1. Wstęp.
2. Wyznaczanie ciągłości funkcji.
3. Klasyfikacja punktów przerwania
4. Własności funkcji ciągłych.
5. Ekonomiczne znaczenie ciągłości.
6. Wniosek.
10.1. Wstęp
Ilekroć oceniamy nieuniknione zmiany w otaczającym nas świecie na przestrzeni czasu, staramy się analizować zachodzące procesy, aby uwypuklić ich najważniejsze cechy. Jedno z pierwszych pytań, które pojawia się na tej ścieżce, brzmi: Jak zachodzą zmiany charakterystyczne dla tego zjawiska - bez przerwy Lub dyskretnie, tj. spazmatycznie. Czy kurs waluty deprecjonuje się lub załamuje równomiernie, czy mamy do czynienia ze stopniową ewolucją, czy może z rewolucyjnym skokiem? Aby ujednolicić ocenę jakościową i ilościową tego, co się dzieje, należy abstrahować od konkretnej treści i badać problem pod kątem zależności funkcjonalnych. Można tego dokonać za pomocą teorii granic, o której mówiliśmy w ostatnim wykładzie.
10.2. Definicja ciągłości funkcji
Ciągłość funkcji intuicyjnie wiąże się z faktem, że jej wykres jest krzywą ciągłą, która nigdzie się nie załamuje. Rysujemy wykres takiej funkcji nie odrywając pióra od papieru. Jeśli funkcja jest podana w tabeli, to ściśle rzecz biorąc, nie można ocenić jej ciągłości, ponieważ dla danego kroku tabeli nie jest określone zachowanie funkcji w przedziałach.
W rzeczywistości przy ciągłości ma miejsce następująca okoliczność: jeżeli parametry charakteryzujące sytuację Trochę to zmień Trochę sytuacja się zmieni. Ważne jest tu nie to, że sytuacja się zmieni, ale to, że zmieni się „trochę”.
Sformułujmy pojęcie ciągłości w języku przyrostów. Niech jakieś zjawisko będzie opisane funkcją i punktem A należy do dziedziny definicji funkcji. Różnica nazywa się przyrost argumentu w tym punkcie A, różnica - przyrost funkcji w tym punkcie A.
Definicja 10.1.Funkcjonować ciągły w pewnym punkcie a, jeśli jest to zdefiniowane w tym miejscu i nieskończenie mały przyrost argumentu odpowiada nieskończenie małemu przyrostowi funkcji:
 Przykład 10.1. Zbadaj ciągłość funkcji w tym punkcie.
Przykład 10.1. Zbadaj ciągłość funkcji w tym punkcie.
Rozwiązanie. Zbudujmy wykres funkcji i zaznaczmy na nim przyrosty D X i D y(ryc. 10.1).
Z wykresu wynika, że im mniejszy jest przyrost D X, tym mniej D y. Pokażmy to analitycznie. Przyrost argumentu jest równy , to przyrost funkcji w tym punkcie będzie równy
Z tego jasno wynika, że jeśli , to i:
![]() .
.
Podajmy inną definicję ciągłości funkcji.
Definicja 10.2.Funkcja nazywa się ciągły w punkcie a jeśli:
1) jest określony w punkcie a i części jego otoczenia;
2) istnieją granice jednostronne i są sobie równe:
![]() ;
;
3) granica funkcji przy x® a jest równe wartości funkcji w tym punkcie:
![]() .
.
Jeśli przynajmniej jeden z tych warunków zostanie naruszony, wówczas mówimy, że funkcja ulega luka.
Definicja ta ma zastosowanie do ustalenia ciągłości w pewnym punkcie. Kierując się jego algorytmem i zwracając uwagę na zbieżności i rozbieżności pomiędzy wymaganiami wyznaczania i konkretny przykład, możemy stwierdzić, że funkcja jest ciągła w tym punkcie.
W Definicji 2 idea bliskości pojawia się wyraźnie, gdy wprowadziliśmy pojęcie granicy. Z nieograniczonym przybliżeniem argumentu X do wartości granicznej A, ciągły w punkcie A funkcjonować F(X) zbliża się do wartości granicznej arbitralnie blisko F(A).
10.3. Klasyfikacja punktów przerwania
Punkty, w których naruszone są warunki ciągłości funkcji, nazywane są punkty przerwania tę funkcję. Jeśli X 0 jest punktem przerwania funkcji, co najmniej jeden z warunków ciągłości funkcji nie jest spełniony. Rozważ następujący przykład.
1. Funkcja jest zdefiniowana w pewnym otoczeniu punktu A, ale nie jest zdefiniowany w samym punkcie A. Na przykład funkcja nie jest zdefiniowana w punkcie A=2, zatem ulega nieciągłości (patrz rys. 10.2).


Ryż. 10.2 Ryc. 10.3
2. Funkcja jest zdefiniowana w punkcie A a w niektórych jego sąsiedztwie istnieją jego jednostronne granice, ale nie są sobie równe: ![]() , to funkcja ulega nieciągłości. Na przykład funkcja
, to funkcja ulega nieciągłości. Na przykład funkcja
![]()
jest zdefiniowana w punkcie, ale w funkcji występuje nieciągłość (patrz rys. 10.3), ponieważ
![]() I
I ![]() ().
().
3. Funkcja jest zdefiniowana w punkcie A i w pewnym jej sąsiedztwie istnieje granica funkcji w , ale ta granica nie jest równa wartości funkcji w punkcie A:
![]() .
.
Na przykład funkcja (patrz ryc. 10.4)


Oto punkt krytyczny:
![]() ,
,
Wszystkie punkty nieciągłości dzielą się na usuwalne punkty nieciągłości, punkty nieciągłości pierwszego i drugiego rodzaju.
Definicja 10.1. Punkt przerwania nazywany jest punktem naprawialna luka , jeśli w tym punkcie istnieją skończone granice funkcji po lewej i prawej stronie, równe sobie:
![]() .
.
Granica funkcji w tym punkcie istnieje, ale nie jest równa wartości funkcji w punkcie granicznym (jeśli funkcja jest zdefiniowana w punkcie granicznym) lub funkcja w punkcie granicznym nie jest zdefiniowana.
Na ryc. 10.4 w momencie naruszenia warunków ciągłości i funkcja ma nieciągłość. Punkt na wykresie (0; 1) wydłubane. Jednak tę lukę można łatwo wyeliminować - wystarczy przedefiniować tę funkcję, ustawiając ją na wartość równą jej granicy w tym punkcie, tj. umieścić . Dlatego takie luki nazywane są usuwalnymi.
Definicja 10.2. Punkt krytyczny nazywa się punkt nieciągłości pierwszego rodzaju , jeśli w tym punkcie istnieją skończone granice funkcji po lewej i prawej stronie, ale nie są one sobie równe:
![]() .
.
W tym momencie mówimy, że funkcja doświadcza skok.
Na ryc. 10.3 funkcja ma w punkcie nieciągłość pierwszego rodzaju. Granice lewa i prawa w tym punkcie są równe:
![]() I
I ![]() .
.
Skok funkcji w punkcie nieciągłości jest równy .
Nie da się zdefiniować takiej funkcji jako ciągłej. Wykres składa się z dwóch półprostych oddzielonych skokiem.
Definicja 10.3. Punkt krytyczny nazywa się punkt nieciągłości II rodzaju , jeśli choć jedna z jednostronnych granic funkcji (lewa lub prawa) nie istnieje lub jest równa nieskończoności.
Na rysunku 10.3 funkcja w punkcie ma nieciągłość drugiego rodzaju. Rozważana funkcja at jest nieskończenie duża i nie ma skończonej granicy ani po prawej, ani po lewej stronie. Nie ma więc w takim momencie mowy o ciągłości.
Przykład 10.2. Zbuduj wykres i określ charakter punktów przerwania:


Rozwiązanie. Narysujmy funkcję F(X) (Rysunek 10.5).
Z rysunku wynika, że pierwotna funkcja ma trzy punkty nieciągłości: , X 2 = 1,
X 3 = 3. Rozważmy je w kolejności.
Dlatego o to chodzi pęknięcie II rodzaju.
a) Funkcja jest zdefiniowana w tym miejscu: F(1) = –1.
B) ![]() , ,
, ,
te. w tym punkcie X 2 = 1 dostępny naprawialna luka. Redefiniując wartość funkcji w tym momencie: F(1) = 5, nieciągłość jest eliminowana i funkcja w tym punkcie staje się ciągła.
a) Funkcja jest zdefiniowana w tym miejscu: F(3) = 1.
A więc w punkcie X 1 = 3 dostępne pęknięcie I rodzaju. Funkcja w tym momencie doświadcza skoku równego D y= –2–1 = –3.
10.4. Własności funkcji ciągłych
Przywołując odpowiednie właściwości granic, dochodzimy do wniosku, że funkcje będące wynikiem działań arytmetycznych na funkcjach ciągłych w tym samym punkcie są również ciągłe. Notatka:
1) jeśli funkcje i są ciągłe w punkcie A, to funkcje , i (pod warunkiem, że ) są również ciągłe w tym punkcie;
2) jeśli funkcja jest ciągła w punkcie A a funkcja jest wówczas ciągła w tym punkcie złożona funkcja ciągły w pewnym punkcie A I
![]() ,
,
te. znak graniczny można umieścić pod znakiem funkcji ciągłej.
Mówią, że funkcja jest ciągła w pewnym zbiorze, jeśli jest ciągła w każdym punkcie tego zbioru. Wykres takiej funkcji jest linią ciągłą, którą można przekreślić jednym pociągnięciem pióra.
Wszystkich głównych funkcje elementarne ciągłe we wszystkich punktach, w których są zdefiniowane.
Funkcje, ciągłe na segmencie, mają wiele ważnych charakterystyczne właściwości. Sformułujmy twierdzenia wyrażające niektóre z tych własności.
Twierdzenie 10.1 (Twierdzenie Weierstrassa ). Jeśli funkcja jest ciągła w segmencie, to osiąga w tym segmencie swoje wartości minimalne i maksymalne.
Twierdzenie 10.2 (Twierdzenie Cauchy'ego ). Jeśli funkcja jest ciągła na pewnym przedziale, to w tym przedziale znajdują się wszystkie wartości pośrednie między najmniejszą i największą wartością.
Z twierdzenia Cauchy'ego wynika następująca ważna własność.
Twierdzenie 10.3. Jeżeli funkcja jest ciągła na odcinku i przyjmuje wartości różnych znaków na końcach odcinka, to pomiędzy a i b znajduje się punkt c, w którym funkcja zanika:.
 Znaczenie geometryczne Twierdzenie to jest oczywiste: jeśli wykres funkcji ciągłej przechodzi z dolnej półpłaszczyzny do górnej półpłaszczyzny (lub odwrotnie), to przynajmniej w jednym punkcie przetnie oś Wół(ryc. 10.6).
Znaczenie geometryczne Twierdzenie to jest oczywiste: jeśli wykres funkcji ciągłej przechodzi z dolnej półpłaszczyzny do górnej półpłaszczyzny (lub odwrotnie), to przynajmniej w jednym punkcie przetnie oś Wół(ryc. 10.6).
Przykład 10.3. Oblicz w przybliżeniu pierwiastek równania
![]() , (tj. w przybliżeniu zastąpić) wielomian odpowiedniego stopnia.
, (tj. w przybliżeniu zastąpić) wielomian odpowiedniego stopnia.
Jest to bardzo ważna w praktyce właściwość funkcji ciągłych. Na przykład bardzo często funkcje ciągłe są określone w tabelach (dane obserwacyjne lub eksperymentalne). Następnie, stosując jakąś metodę, można zastąpić funkcję tabelaryczną wielomianem. Zgodnie z Twierdzeniem 10.3 można to zawsze zrobić z wystarczająco dużą dokładnością. Praca z funkcją zdefiniowaną analitycznie (zwłaszcza wielomianem) jest znacznie łatwiejsza.
10,5. Ekonomiczne znaczenie ciągłości
Większość funkcji stosowanych w ekonomii ma charakter ciągły, co pozwala na sformułowanie dość znaczących stwierdzeń o treści ekonomicznej.
Aby to zilustrować, rozważmy następujący przykład.
Wysokość podatku N ma w przybliżeniu taki sam wykres jak na ryc. 10.7a.

Na końcach przedziałów jest ona nieciągła i nieciągłości te są I rodzaju. Jednak sama wartość podatek dochodowy P(Rys. 10.7b) jest ciągłą funkcją rocznego dochodu Q. Stąd w szczególności wynika, że jeśli roczne dochody dwóch osób różnią się nieznacznie, to różnica w kwotach podatku dochodowego, który muszą zapłacić, również powinna się nieznacznie różnić. Co ciekawe, okoliczność ta jest postrzegana przez zdecydowaną większość ludzi jako całkowicie naturalna, o czym nawet nie myślą.
10.6. Wniosek
Na koniec pozwólmy sobie na mały odwrót.
Oto jak graficznie wyrazić smutną obserwację starożytnych:
Sic tranzyt Gloria mundi...
(Tak to działa ziemska chwała …)

Koniec pracy -
Ten temat należy do działu:
Pojęcie funkcji
Pojęcie funkcji.. wszystko płynie i wszystko się zmienia Heraklit.. stół x x x x y y y y..
Jeśli potrzebujesz dodatkowy materiał na ten temat lub nie znalazłeś tego, czego szukałeś, polecamy skorzystać z wyszukiwarki w naszej bazie dzieł:
Co zrobimy z otrzymanym materiałem:
Jeśli ten materiał był dla Ciebie przydatny, możesz zapisać go na swojej stronie w sieciach społecznościowych:
Niech chodzi A należy do obszaru specyfikacji funkcji k(x) i jakikolwiek ε -sąsiedztwo punktu A zawiera różne od A punkty obszaru definicji funkcji k(x), tj. kropka A to punkt graniczny zbioru (X), na którym określona jest funkcja k(x).
Definicja. Funkcjonować k(x) nazywany ciągłym w punkcie A, jeśli funkcja k(x) ma w tym punkcie A limit i ten limit jest równy określonej wartości fa) Funkcje k(x) w tym punkcie A.
Z tej definicji wynika, co następuje warunek ciągłości funkcji k(x) w tym punkcie A :
Od , wtedy możemy pisać
![]()
Dlatego dla linii ciągłej w punkcie A pełni funkcję symbolu przejścia granicznego i symbolu F charakterystyki funkcji można zamieniać.
Definicja. Funkcjonować k(x) nazywa się ciągłym po prawej (lewej) stronie punktu A, jeśli prawa (lewa) granica tej funkcji w punkcie A istnieje i jest równa wartości prywatnej fa) Funkcje k(x) w tym punkcie A.
Fakt, że funkcja k(x) ciągły w pewnym punkcie A po prawej stronie napisz to tak:
I ciągłość funkcji k(x) w tym punkcie A po lewej stronie zapisano jako:
Komentarz. Punkty, w których funkcja nie ma własności ciągłości, nazywane są punktami nieciągłości tej funkcji.
Twierdzenie. Niech funkcje będą dane na tym samym zbiorze k(x) I g(x), ciągły w punkcie A. Następnie funkcje f(x)+g(x), f(x)-g(x), f(x) g(x) I f(x)/g(x)- ciągły w punkcie A(w przypadku prywatnego trzeba dodatkowo wymagać g(a) ≠ 0).
Ciągłość podstawowych funkcji elementarnych
1) Funkcja zasilania y=xn z naturalnym N ciągły na całej osi liczbowej.
Najpierw spójrzmy na funkcję f(x)=x. Według pierwszej definicji granicy funkcji w punkcie A weź dowolną sekwencję (xn), zbiegający się do A, a następnie odpowiednia sekwencja wartości funkcji (f(xn)=xn) zbiegnie się również do A, to jest ![]() , czyli funkcja f(x)=x ciągły w dowolnym punkcie osi liczbowej.
, czyli funkcja f(x)=x ciągły w dowolnym punkcie osi liczbowej.
Rozważmy teraz funkcję f(x)=x n, Gdzie N - Liczba naturalna, Następnie f(x)=x · x · … · x. Przejdźmy do limitu o godz x → za, otrzymujemy , czyli funkcję f(x)=x n ciągły na osi liczbowej.
2) Funkcja wykładnicza.
Funkcja wykładnicza y=ax Na a>1 jest funkcją ciągłą w dowolnym punkcie nieskończonej prostej.
Funkcja wykładnicza y=ax Na a>1 spełnia warunki:
3) Funkcja logarytmiczna.
Funkcja logarytmiczna jest ciągła i rośnie wzdłuż całej półprostej x>0 Na a>1 i jest ciągły i maleje wzdłuż całej półprostej x>0 Na 0
4) Funkcje hiperboliczne.
Następujące funkcje nazywane są funkcjami hiperbolicznymi:
Z definicji funkcji hiperbolicznych wynika, że cosinus hiperboliczny, sinus hiperboliczny i tangens hiperboliczny są zdefiniowane na całej osi liczbowej, a cotangens hiperboliczny jest zdefiniowany wszędzie na osi liczbowej, z wyjątkiem punktu x=0.
Funkcje hiperboliczne są ciągłe w każdym punkcie swojej dziedziny (wynika to z ciągłości funkcji wykładniczej i twierdzenia o działaniach arytmetycznych).
5) Funkcja mocy
Funkcja zasilania y=x α =a α log a x ciągły w każdym punkcie otwartej półprostej x>0.
6) Funkcje trygonometryczne.
Funkcje grzech x I bo x ciągły w każdym punkcie X nieskończoną linię prostą. Funkcjonować y = opalenizna x (kπ-π/2,kπ+π/2) i funkcja y=ctg x ciągły w każdym przedziale ((k-1)π,kπ)(wszędzie tutaj k- dowolna liczba całkowita, tj. k=0, ±1, ±2, …).
7) Odwrotne funkcje trygonometryczne.
Funkcje y = arcsin x I y=arccos x ciągły w segmencie [-1, 1] . Funkcje y=arctg x I y=łuk x ciągły na nieskończonej linii.
Dwie wspaniałe granice
Twierdzenie. Granica funkcji (grzech x)/x w tym punkcie x=0 istnieje i jest równy jeden, tj.
![]()
Limit ten nazywa się pierwszy niezwykły limit.
Dowód. Na 0
![]()
![]()
Nierówności te obowiązują także dla wartości X, spełniający warunki -π/2 ![]() . Ponieważ bo x jest zatem funkcją ciągłą
. Ponieważ bo x jest zatem funkcją ciągłą ![]() . Zatem dla funkcji bo x, 1 i w niektórych δ
-sąsiedztwo punktu x=0 wszystkie warunki twierdzeń są spełnione. Stąd,
. Zatem dla funkcji bo x, 1 i w niektórych δ
-sąsiedztwo punktu x=0 wszystkie warunki twierdzeń są spełnione. Stąd, ![]() .
.
Twierdzenie. Granica funkcji ![]() Na x → ∞ istnieje i jest równa liczbie mi:
Na x → ∞ istnieje i jest równa liczbie mi:
![]()
Limit ten nazywa się drugi niezwykły limit.
Komentarz. Prawdą jest również, że
![]()
Ciągłość funkcji zespolonej
Twierdzenie. Niech funkcja x=φ(t) ciągły w pewnym punkcie A i funkcja y=f(x) ciągły w pewnym punkcie b=φ(a). Następnie funkcja złożona y=f[φ(t)]=F(t) ciągły w pewnym punkcie A.
Pozwalać x=φ(t) I y=f(x)- najprostsze funkcje elementarne, z wieloma wartościami (X) Funkcje x=φ(t) jest zakresem funkcji y=f(x). Jak wiemy, funkcje elementarne są ciągłe w każdym punkcie danej dziedziny. Dlatego, zgodnie z poprzednim twierdzeniem, funkcja zespolona y=f(φ(t)), czyli superpozycja dwóch funkcji elementarnych, jest ciągła. Na przykład funkcja jest ciągła w dowolnym punkcie x ≠ 0, jako złożona funkcja dwóch funkcji elementarnych x=t -1 I y=grzech x. Również funkcjonować y=ln grzech x ciągły w dowolnym punkcie przedziału (2kπ,(2k+1)π), k ∈ Z (grzech x > 0).
Ciągłość funkcji. Punkty załamania.
Byk chodzi, kołysze się, wzdycha po drodze:
- Och, deska się kończy, teraz spadam!
Na tej lekcji zajmiemy się pojęciem ciągłości funkcji, klasyfikacją punktów nieciągłości i powszechnym problemem praktycznym badania ciągłości funkcji. Już od samej nazwy tematu wielu intuicyjnie domyśla się, co będzie omawiane i uważa, że materiał jest dość prosty. To prawda. Jednak to proste zadania są najczęściej karane za zaniedbania i powierzchowne podejście do ich rozwiązywania. Dlatego zalecam bardzo dokładne przestudiowanie artykułu i wyłapanie wszystkich subtelności i technik.
Co musisz wiedzieć i umieć? Nie bardzo. Aby dobrze nauczyć się lekcji, musisz zrozumieć, co to jest granica funkcji. Czytelnikom o niskim poziomie przygotowania wystarczy zrozumienie artykułu Granice funkcji. Przykłady rozwiązań i spójrz na geometryczne znaczenie limitu w instrukcji Wykresy i własności funkcji elementarnych. Wskazane jest również zapoznanie się z przekształcenia geometryczne grafów, ponieważ praktyka w większości przypadków polega na konstruowaniu rysunku. Perspektywy dla wszystkich są optymistyczne i nawet pełny czajnik poradzi sobie sam z zadaniem w ciągu najbliższej godziny lub dwóch!
Ciągłość funkcji. Punkty przerwania i ich klasyfikacja
Pojęcie ciągłości funkcji
Rozważmy pewną funkcję ciągłą na całej osi liczbowej: 
Lub, mówiąc prościej, nasza funkcja jest ciągła na (zbiorze liczb rzeczywistych).
Jakie jest „filistyńskie” kryterium ciągłości? Oczywiście wykres funkcji ciągłej można narysować bez odrywania ołówka od papieru.
W tym przypadku należy wyraźnie rozróżnić dwa proste pojęcia: dziedzina funkcji I ciągłość funkcji. Ogólnie to nie to samo. Na przykład: 
Funkcja ta jest zdefiniowana na całej osi liczbowej, czyli dla wszyscy Znaczenie „x” ma swoje własne znaczenie „y”. W szczególności, jeśli , to . Należy pamiętać, że drugi punkt jest przerywany, ponieważ zgodnie z definicją funkcji wartość argumentu musi odpowiadać Jedyną rzeczą wartość funkcji. Zatem, domena nasza funkcja: .
Jednakże ta funkcja nie jest włączona w sposób ciągły! Jest całkiem oczywiste, że w tym momencie cierpi luka. Określenie to jest również dość zrozumiałe i wizualne, bo w tym przypadku ołówek i tak trzeba będzie oderwać od papieru. Nieco później przyjrzymy się klasyfikacji punktów przerwania.
Ciągłość funkcji w punkcie i na przedziale
W konkretnym problemie matematycznym możemy mówić o ciągłości funkcji w punkcie, ciągłości funkcji na przedziale, półprzedziale lub ciągłości funkcji na odcinku. To jest, nie ma „zwykłej ciągłości”– funkcja może być GDZIEŚ ciągła. Podstawowym „cegiełkiem” wszystkiego innego jest ciągłość funkcji w tym punkcie .
Teoria analizy matematycznej definiuje ciągłość funkcji w punkcie za pomocą sąsiedztwa „delta” i „epsilon”, ale w praktyce stosuje się inną definicję, na którą zwrócimy szczególną uwagę.
Najpierw pamiętajmy jednostronne granice który wdarł się w nasze życie już na pierwszej lekcji o wykresach funkcji. Rozważ codzienną sytuację: 
Jeśli zbliżymy się do osi do punktu lewy(czerwona strzałka), wówczas odpowiednie wartości „gier” przejdą wzdłuż osi do punktu (karmazynowa strzałka). Matematycznie fakt ten ustala się za pomocą lewe ograniczenie:
Zwróć uwagę na wpis (czytaj: „x ma tendencję do ka po lewej stronie”). Symbolizuje „dodatek” „minus zero”. , zasadniczo oznacza to, że zbliżamy się do liczby od lewej strony.
Podobnie, jeśli zbliżysz się do punktu „ka” po prawej(niebieska strzałka), wówczas „gry” osiągną tę samą wartość, ale wzdłuż zielonej strzałki i granica prawa zostanie sformatowany w następujący sposób:
„Dodatek” symbolizuje , a wpis brzmi: „x ma tendencję do ka po prawej stronie”.
Jeśli granice jednostronne są skończone i równe(jak w naszym przypadku): ![]() , to powiemy, że istnieje OGÓLNA granica. To proste, ogólny limit jest naszym „zwykłym” granica funkcji, równa liczbie skończonej.
, to powiemy, że istnieje OGÓLNA granica. To proste, ogólny limit jest naszym „zwykłym” granica funkcji, równa liczbie skończonej.
Należy pamiętać, że jeśli funkcja nie jest zdefiniowana w (wyróżnij czarną kropkę na gałęzi wykresu), to powyższe obliczenia pozostają ważne. Jak już kilkakrotnie zauważono, w szczególności w artykule na nieskończenie małych funkcjach, wyrażenia oznaczają, że „x” nieskończenie blisko zbliża się do punktu, podczas gdy NIE MA ZNACZENIA, niezależnie od tego, czy sama funkcja jest zdefiniowana w danym punkcie, czy nie. Dobry przykład można znaleźć w następnym akapicie, kiedy analizowana jest funkcja.
Definicja: funkcja jest ciągła w punkcie, jeśli granica funkcji w danym punkcie jest równa wartości funkcji w tym punkcie: .
Definicja jest szczegółowo opisana w następujących terminach:
1) Funkcja musi być zdefiniowana w punkcie, czyli wartość musi istnieć.
2) Musi istnieć ogólna granica funkcji. Jak zauważono powyżej, oznacza to istnienie i równość granic jednostronnych: ![]() .
.
3) Granica funkcji w danym punkcie musi być równa wartości funkcji w tym punkcie: .
Jeśli naruszone przynajmniej jeden trzech warunków, wówczas funkcja traci właściwość ciągłości w punkcie .
Ciągłość funkcji w przedziale jest sformułowane pomysłowo i bardzo prosto: funkcja jest ciągła na przedziale, jeśli jest ciągła w każdym punkcie danego przedziału.
W szczególności wiele funkcji jest ciągłych na nieskończonym przedziale, to znaczy na zbiorze liczb rzeczywistych. Jest to funkcja liniowa, wielomiany, wykładnicza, sinus, cosinus itp. I ogólnie dowolna funkcja elementarna ciągły na swoim dziedzina definicji na przykład funkcja logarytmiczna jest ciągła w przedziale . Mamy nadzieję, że masz już całkiem niezłe pojęcie o tym, jak wyglądają wykresy podstawowych funkcji. Bardziej szczegółowe informacje na temat ich ciągłości można uzyskać od życzliwego człowieka nazwiskiem Fichtenholtz.
Przy ciągłości funkcji na odcinku i półprzedziałach wszystko też nie jest trudne, ale lepiej porozmawiać o tym na zajęciach o znalezieniu minimalnej i maksymalnej wartości funkcji w segmencie, ale na razie nie martwmy się tym.
Klasyfikacja punktów przerwania
Fascynujące życie funkcji jest bogate w różnego rodzaju punkty szczególne, a punkty przerwania to tylko jedna ze stron ich biografii.
Notatka : na wszelki wypadek zatrzymam się na punkcie elementarnym: punktem krytycznym jest zawsze pojedyńczy punkt– nie ma „kilku punktów przerwania z rzędu”, czyli nie ma czegoś takiego jak „przerwa”.
Punkty te z kolei dzielą się na dwie duże grupy: pęknięcia pierwszego rodzaju I pęknięcia drugiego rodzaju. Każdy rodzaj luki ma swoje charakterystyczne cechy, którym teraz się przyjrzymy:
Punkt nieciągłości pierwszego rodzaju
Jeśli w pewnym momencie zostanie naruszony warunek ciągłości i jednostronne granice skończone , wtedy to się nazywa punkt nieciągłości pierwszego rodzaju.
Zacznijmy od najbardziej optymistycznego przypadku. Zgodnie z pierwotną ideą lekcji chciałem opowiedzieć teorię „w kategoriach ogólnych”, ale aby wykazać realność materiału, zdecydowałem się na opcję z określonymi postaciami.
To smutne, jak zdjęcie nowożeńców na tle Wiecznego Płomienia, ale poniższe ujęcie jest powszechnie akceptowane. Przedstawmy wykres funkcji na rysunku: 
Funkcja ta jest ciągła na całej osi liczbowej z wyjątkiem punktu. I w rzeczywistości mianownik nie może być równy zero. Jednak zgodnie ze znaczeniem limitu możemy nieskończenie blisko zbliżaj się do „zera” zarówno od lewej, jak i od prawej strony, to znaczy istnieją jednostronne granice i oczywiście pokrywają się: ![]() (Warunek nr 2 ciągłości jest spełniony).
(Warunek nr 2 ciągłości jest spełniony).
Jednak funkcja nie jest zdefiniowana w tym punkcie, dlatego też warunek nr 1 ciągłości zostaje naruszony i funkcja w tym miejscu cierpi na nieciągłość.
Przerwa tego typu (z istniejącym ogólny limit) są nazywane naprawialna luka. Dlaczego wyjmowany? Ponieważ funkcja może przedefiniować w punkcie krytycznym: 
Czy to wygląda dziwnie? Może. Ale taki zapis funkcji w niczym nie zaprzecza! Teraz luka została zamknięta i wszyscy są szczęśliwi: 
Przeprowadźmy kontrolę formalną:
2) ![]() – istnieje ogólny limit;
– istnieje ogólny limit;
3)
Zatem wszystkie trzy warunki są spełnione, a funkcja jest ciągła w punkcie z definicji ciągłości funkcji w punkcie.
Jednak hejterzy matan mogą na przykład źle zdefiniować funkcję 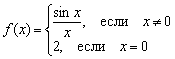 :
:
Co ciekawe, spełnione są tutaj dwa pierwsze warunki ciągłości:
1) – funkcja jest zdefiniowana w danym punkcie;
2) ![]() – istnieje ogólne ograniczenie.
– istnieje ogólne ograniczenie.
Ale trzecia granica nie została przekroczona: , czyli granica funkcji w punkcie nie równe wartość danej funkcji w danym punkcie.
Zatem w pewnym momencie funkcja wykazuje nieciągłość.
Drugi, smutniejszy przypadek to tzw pęknięcie pierwszego rodzaju ze skokiem. A smutek jest wywoływany przez jednostronne ograniczenia skończone i różne. Przykład pokazano na drugim rysunku lekcji. Taka luka zwykle występuje w funkcje określone fragmentarycznie, o których była już mowa w artykule o przekształceniach grafów.
Rozważmy funkcję fragmentaryczną  i uzupełnimy jego rysunek. Jak zbudować wykres? Bardzo prosta. Na półodcinku rysujemy fragment paraboli (kolor zielony), na przedziale odcinek prosty (kolor czerwony), a na połowie odcinka linię prostą (kolor niebieski).
i uzupełnimy jego rysunek. Jak zbudować wykres? Bardzo prosta. Na półodcinku rysujemy fragment paraboli (kolor zielony), na przedziale odcinek prosty (kolor czerwony), a na połowie odcinka linię prostą (kolor niebieski).
Ponadto ze względu na nierówność wyznaczana jest wartość dla funkcji kwadratowej (zielona kropka), a ze względu na nierówność wartość jest wyznaczana dla funkcji liniowej (niebieska kropka): 
W najtrudniejszym przypadku należy zastosować konstrukcję punkt po punkcie każdego fragmentu wykresu (patrz pierwszy lekcja o wykresach funkcji).
Teraz będzie nas interesować tylko ten punkt. Zbadajmy to pod kątem ciągłości:
2) Obliczmy granice jednostronne.
Po lewej stronie mamy odcinek czerwonej linii, zatem lewa granica wynosi: ![]()
Po prawej stronie znajduje się niebieska linia prosta i prawa granica: ![]()
W rezultacie otrzymaliśmy skończone liczby, i oni nie równe. Ponieważ jednostronne granice skończone i różne: ![]() , to nasza funkcja toleruje nieciągłość pierwszego rodzaju ze skokiem.
, to nasza funkcja toleruje nieciągłość pierwszego rodzaju ze skokiem.
Logiczne jest, że luki nie można wyeliminować - funkcji tak naprawdę nie można dalej zdefiniować i „skleić”, jak w poprzednim przykładzie.
Punkty nieciągłości drugiego rodzaju
Zwykle wszystkie inne przypadki pęknięcia są sprytnie klasyfikowane do tej kategorii. Nie będę wymieniał wszystkiego, bo w praktyce w 99% problemów się spotkasz niekończąca się przepaść– gdy jest się leworęcznym lub praworęcznym, a częściej obie granice są nieskończone.
I oczywiście najbardziej oczywistym obrazem jest hiperbola w punkcie zerowym. Tutaj obie jednostronne granice są nieskończone: ![]() , zatem funkcja cierpi na nieciągłość drugiego rodzaju w punkcie .
, zatem funkcja cierpi na nieciągłość drugiego rodzaju w punkcie .
Staram się wypełniać swoje artykuły możliwie różnorodną treścią, dlatego przyjrzyjmy się wykresowi funkcji, która jeszcze nie została napotkana: 
według standardowego schematu:
1) Funkcja nie jest w tym momencie zdefiniowana, ponieważ mianownik dąży do zera.
Oczywiście możemy od razu stwierdzić, że funkcja ma nieciągłość w punkcie , ale dobrze byłoby sklasyfikować charakter nieciągłości, czego często wymaga warunek. Dla tego:

Przypomnę, że pisząc mamy na myśli nagrywanie nieskończenie mała liczba ujemna, a pod wpisem - nieskończenie mała liczba dodatnia.
Granice jednostronne są nieskończone, co oznacza, że funkcja ma w punkcie nieciągłość II rodzaju. Oś Y jest pionowa asymptota dla wykresu.
Nierzadko zdarza się, że istnieją obie jednostronne granice, ale tylko jedna z nich jest nieskończona, na przykład: 
To jest wykres funkcji.
Badamy punkt ciągłości:
1) Funkcja nie jest w tym momencie zdefiniowana.
2) Obliczmy granice jednostronne: 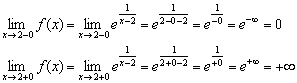
O sposobie obliczania takich jednostronnych granic porozmawiamy w dwóch ostatnich przykładach wykładu, choć wielu czytelników już wszystko widziało i domyślało się.
Lewa granica jest skończona i równa zeru („nie idziemy do samego punktu”), ale prawa granica jest nieskończona i pomarańczowa gałąź wykresu zbliża się nieskończenie blisko swojej pionowa asymptota, podane równaniem (czarna linia przerywana).
Zatem funkcja cierpi nieciągłość drugiego rodzaju W punkcie .
W przypadku nieciągłości pierwszego rodzaju funkcję można zdefiniować w samym punkcie nieciągłości. Na przykład dla funkcji fragmentarycznej  Możesz umieścić czarną, pogrubioną kropkę na początku współrzędnych. Po prawej stronie znajduje się gałąź hiperboli, a prawa granica jest nieskończona. Myślę, że prawie każdy ma pojęcie, jak wygląda ten wykres.
Możesz umieścić czarną, pogrubioną kropkę na początku współrzędnych. Po prawej stronie znajduje się gałąź hiperboli, a prawa granica jest nieskończona. Myślę, że prawie każdy ma pojęcie, jak wygląda ten wykres.
To na co wszyscy czekali:
Jak sprawdzić ciągłość funkcji?
Badanie funkcji na ciągłość w punkcie przeprowadza się według ustalonego już rutynowego schematu, który polega na sprawdzeniu trzech warunków ciągłości:
Przykład 1
Przeglądaj funkcję ![]()
Rozwiązanie:
1) Jedynym punktem w zakresie jest sytuacja, w której funkcja nie jest zdefiniowana.
2) Obliczmy granice jednostronne: 
Granice jednostronne są skończone i równe.
Zatem w tym punkcie funkcja cierpi na usuwalną nieciągłość.
Jak wygląda wykres tej funkcji?
Chciałbym uprościć ![]() i wygląda na to, że otrzymano zwykłą parabolę. ALE pierwotna funkcja nie jest zdefiniowana w punkcie , dlatego wymagana jest następująca klauzula:
i wygląda na to, że otrzymano zwykłą parabolę. ALE pierwotna funkcja nie jest zdefiniowana w punkcie , dlatego wymagana jest następująca klauzula:
Zróbmy rysunek: 
Odpowiedź: funkcja jest ciągła na całej osi liczbowej z wyjątkiem punktu, w którym występuje usuwalna nieciągłość.
Funkcję można dalej zdefiniować w dobry lub niezbyt dobry sposób, ale w zależności od warunku nie jest to wymagane.
Mówisz, że to naciągany przykład? Zupełnie nie. W praktyce zdarzało się to dziesiątki razy. Prawie wszystkie zadania serwisu pochodzą z prawdziwej, niezależnej pracy i testów.
Pozbądźmy się naszych ulubionych modułów:
Przykład 2
Przeglądaj funkcję ![]() dla ciągłości. Określić charakter nieciągłości funkcji, jeśli istnieją. Wykonaj rysunek.
dla ciągłości. Określić charakter nieciągłości funkcji, jeśli istnieją. Wykonaj rysunek.
Rozwiązanie: Z jakiegoś powodu uczniowie boją się i nie lubią funkcji z modułem, chociaż nie ma w nich nic skomplikowanego. Już trochę poruszaliśmy te tematy na lekcji. Przekształcenia geometryczne grafów. Ponieważ moduł jest nieujemny, rozwija się go w następujący sposób: ![]() , gdzie „alfa” jest pewnym wyrażeniem. W tym przypadku naszą funkcję należy zapisać fragmentarycznie:
, gdzie „alfa” jest pewnym wyrażeniem. W tym przypadku naszą funkcję należy zapisać fragmentarycznie: 
Ale ułamki obu części muszą zostać zmniejszone o . Redukcja, podobnie jak w poprzednim przykładzie, nie odbędzie się bez konsekwencji. Funkcja pierwotna nie jest zdefiniowana w tym punkcie, ponieważ mianownik dąży do zera. Dlatego system powinien dodatkowo określić warunek i uczynić pierwszą nierówność ścisłą: 
A teraz o BARDZO PRZYDATNEJ technice decyzyjnej: przed sfinalizowaniem zadania na szkicu warto wykonać rysunek (niezależnie od tego, czy wymagają tego warunki, czy nie). Pomoże to, po pierwsze, od razu dostrzec punkty ciągłości i nieciągłości, a po drugie, w 100% uchroni Cię przed błędami przy znajdowaniu granic jednostronnych.
Zróbmy rysunek. Zgodnie z naszymi obliczeniami, na lewo od punktu należy narysować fragment paraboli (kolor niebieski), a na prawo fragment paraboli (kolor czerwony), natomiast funkcja nie jest zdefiniowana na sam wskaż: 
Jeśli masz wątpliwości, weź kilka wartości x i podłącz je do funkcji ![]() (pamiętając, że moduł niszczy ewentualny znak minus) i sprawdź wykres.
(pamiętając, że moduł niszczy ewentualny znak minus) i sprawdź wykres.
Zbadajmy analitycznie funkcję ciągłości:
1) Funkcja nie jest w punkcie zdefiniowana, więc od razu można powiedzieć, że nie jest w tym miejscu ciągła.
2) Ustalmy naturę nieciągłości, w tym celu obliczamy granice jednostronne: 
Granice jednostronne są skończone i różne, co oznacza, że funkcja doznaje nieciągłości pierwszego rodzaju ze skokiem w punkcie . Należy jeszcze raz zauważyć, że przy znajdowaniu granic nie ma znaczenia, czy funkcja w punkcie przerwania jest zdefiniowana, czy nie.
Teraz pozostaje tylko przenieść rysunek z szkicu (został wykonany jakby na podstawie badań ;-)) i wykonać zadanie:
Odpowiedź: funkcja jest ciągła na całej osi liczbowej z wyjątkiem punktu, w którym wraz ze skokiem następuje nieciągłość pierwszego rodzaju.
Czasami wymagają dodatkowego wskazania skoku nieciągłości. Oblicza się to prosto - od prawej granicy należy odjąć lewą granicę: , czyli w punkcie przerwania nasza funkcja przeskoczyła o 2 jednostki w dół (jak mówi nam znak minus).
Przykład 3
Przeglądaj funkcję ![]() dla ciągłości. Określić charakter nieciągłości funkcji, jeśli istnieją. Narysuj coś.
dla ciągłości. Określić charakter nieciągłości funkcji, jeśli istnieją. Narysuj coś.
Jest to przykład do samodzielnego rozwiązania, przykładowe rozwiązanie na końcu lekcji.
Przejdźmy do najpopularniejszej i najbardziej rozpowszechnionej wersji zadania, gdy funkcja składa się z trzech części:
Przykład 4
Zbadaj ciągłość funkcji i narysuj jej wykres  .
.
Rozwiązanie: oczywiste jest, że wszystkie trzy części funkcji są ciągłe w odpowiednich przedziałach, zatem pozostaje sprawdzić tylko dwa punkty „połączenia” pomiędzy częściami. Na początek zróbmy szkic, technikę konstrukcyjną wystarczająco szczegółowo opisałem w pierwszej części artykułu. Jedyną rzeczą jest to, że musimy uważnie śledzić nasze punkty osobliwe: ze względu na nierówność wartość należy do linii prostej (zielona kropka), a ze względu na nierówność wartość należy do paraboli (czerwona kropka): 
Cóż, w zasadzie wszystko jest jasne =) Pozostaje tylko sformalizować decyzję. Dla każdego z dwóch punktów „łączenia” standardowo sprawdzamy 3 warunki ciągłości:
I) Badamy punkt pod kątem ciągłości
1) ![]()

Granice jednostronne są skończone i różne, co oznacza, że funkcja doznaje nieciągłości pierwszego rodzaju ze skokiem w punkcie .
Obliczmy skok nieciągłości jako różnicę między prawą i lewą granicą:
oznacza to, że wykres podskoczył o jedną jednostkę.
II) Badamy punkt pod kątem ciągłości
1) ![]() – funkcja jest zdefiniowana w danym punkcie.
– funkcja jest zdefiniowana w danym punkcie.
2) Znajdź granice jednostronne: 
![]() – granice jednostronne są skończone i równe, co oznacza, że istnieje granica ogólna.
– granice jednostronne są skończone i równe, co oznacza, że istnieje granica ogólna.
3) ![]() – granica funkcji w punkcie jest równa wartości tej funkcji w danym punkcie.
– granica funkcji w punkcie jest równa wartości tej funkcji w danym punkcie.
Na ostatnim etapie przenosimy rysunek do wersji ostatecznej, po czym umieszczamy ostateczny akord:
Odpowiedź: funkcja jest ciągła na całej osi liczbowej, z wyjątkiem punktu, w którym wraz ze skokiem następuje nieciągłość pierwszego rodzaju.
Przykład 5
Zbadaj ciągłość funkcji i skonstruuj jej wykres  .
.
Jest to przykład samodzielnego rozwiązania, krótkie rozwiązanie i przybliżona próbka problemu na końcu lekcji.
Można odnieść wrażenie, że w jednym punkcie funkcja musi być ciągła, a w innym musi być nieciągłość. W praktyce nie zawsze tak jest. Staraj się nie zaniedbywać pozostałych przykładów - będzie kilka interesujących i ważnych funkcji:
Przykład 6
Biorąc pod uwagę funkcję  . Zbadaj funkcję ciągłości w punktach. Zbuduj wykres.
. Zbadaj funkcję ciągłości w punktach. Zbuduj wykres.
Rozwiązanie: i ponownie natychmiast wykonaj rysunek na szkicu: 
Osobliwością tego wykresu jest to, że funkcja odcinkowa jest określona przez równanie osi odciętych. Tutaj obszar ten jest narysowany na zielono, ale w notatniku jest zwykle zaznaczany pogrubioną czcionką za pomocą prostego ołówka. I oczywiście nie zapomnij o naszych baranach: wartość należy do gałęzi stycznej (czerwona kropka), a wartość należy do linii prostej.
Z rysunku wszystko jest jasne - funkcja jest ciągła na całej osi liczbowej, pozostaje tylko sformalizować rozwiązanie, które doprowadza się do pełnej automatyzacji dosłownie po 3-4 podobnych przykładach:
I) Badamy punkt pod kątem ciągłości
1) – funkcja jest zdefiniowana w danym punkcie.
2) Obliczmy granice jednostronne: 
![]() , co oznacza, że istnieje ogólna granica.
, co oznacza, że istnieje ogólna granica.
Na wszelki wypadek przypomnę banalny fakt: granica stałej jest równa samej stałej. W tym przypadku granica zera jest równa samemu zero (granica lewoskrętna).
3) ![]() – granica funkcji w punkcie jest równa wartości tej funkcji w danym punkcie.
– granica funkcji w punkcie jest równa wartości tej funkcji w danym punkcie.
Zatem funkcja jest ciągła w punkcie zgodnie z definicją ciągłości funkcji w punkcie.
II) Badamy punkt pod kątem ciągłości
1) – funkcja jest zdefiniowana w danym punkcie.
2) Znajdź granice jednostronne: 
I tutaj – granica jedności jest równa samej jednostce.
![]() – istnieje ogólne ograniczenie.
– istnieje ogólne ograniczenie.
3)  – granica funkcji w punkcie jest równa wartości tej funkcji w danym punkcie.
– granica funkcji w punkcie jest równa wartości tej funkcji w danym punkcie.
Zatem funkcja jest ciągła w punkcie zgodnie z definicją ciągłości funkcji w punkcie.
Tradycyjnie po badaniach przenosimy nasz rysunek do wersji ostatecznej.
Odpowiedź: funkcja jest ciągła w punktach.
Należy pamiętać, że pod warunkiem, że nie zapytano nas o nic o badanie całej funkcji na ciągłość i uważa się, że jest to dobra forma matematyczna do sformułowania precyzyjne i jasne odpowiedź na zadane pytanie. Swoją drogą, jeśli warunki nie wymagają od Ciebie zbudowania wykresu, to masz pełne prawo go nie budować (choć później nauczyciel może Cię do tego zmusić).
Mały matematyczny „łamacz języka” do samodzielnego rozwiązania:
Przykład 7
Biorąc pod uwagę funkcję 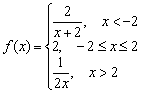 . Zbadaj funkcję ciągłości w punktach. Sklasyfikuj punkty przerwania, jeśli występują. Wykonaj rysunek.
. Zbadaj funkcję ciągłości w punktach. Sklasyfikuj punkty przerwania, jeśli występują. Wykonaj rysunek.
Spróbuj poprawnie „wymówić” wszystkie „słowa” =) I narysuj wykres dokładniej, z dokładnością, nie będzie to wszędzie zbędne ;-)
Jak pamiętacie, zalecałem natychmiastowe uzupełnienie rysunku w wersji roboczej, ale czasami zdarzają się przykłady, w których nie można od razu zorientować się, jak wygląda wykres. Dlatego w niektórych przypadkach korzystne jest najpierw znalezienie jednostronnych granic, a dopiero potem na podstawie badania zobrazowanie gałęzi. W dwóch ostatnich przykładach nauczymy się także techniki obliczania limitów jednostronnych:
Przykład 8
Zbadaj ciągłość funkcji i skonstruuj jej schematyczny wykres.
Rozwiązanie: złe punkty są oczywiste: (redukuje mianownik wykładnika do zera) i (redukuje mianownik całego ułamka do zera). Nie jest jasne, jak wygląda wykres tej funkcji, dlatego lepiej najpierw przeprowadzić pewne badania.
Funkcje ciągłe stanowią główną klasę funkcji, z którymi operuje analiza matematyczna. Ideę funkcji ciągłej można uzyskać mówiąc, że jej wykres jest ciągły, tj. można go narysować bez odrywania ołówka od papieru.
Funkcja ciągła wyraża matematycznie jedną właściwość, z którą często spotykamy się w praktyce, a mianowicie to, że mały przyrost zmiennej niezależnej odpowiada małemu przyrostowi zmiennej zależnej (funkcji). Doskonałymi przykładami funkcji ciągłej mogą być różne prawa ruchu ciał \(s=f(t)\), wyrażające zależność drogi pokonywanej przez ciało od czasu \(t\). Czas i przestrzeń są ciągłe, podczas gdy to czy inne prawo ruchu ciała \(s=f(t)\) ustanawia między nimi pewne ciągłe połączenie, charakteryzujące się tym, że małemu przyrostowi czasu odpowiada mały przyrost drogi.
Człowiek doszedł do abstrakcji ciągłości obserwując otaczające go tzw. ośrodki ciągłe – stałe, ciekłe lub gazowe, np. metale, wodę, powietrze. W rzeczywistości, jak powszechnie wiadomo, każde medium fizyczne jest nagromadzeniem dużej liczby poruszających się cząstek oddzielonych od siebie. Jednakże cząstki te i odległości między nimi są na tyle małe w porównaniu z objętościami ośrodków, z którymi mamy do czynienia w makroskopowych zjawiskach fizycznych, że wiele takich zjawisk można całkiem dobrze zbadać, jeśli przyjmiemy w przybliżeniu masę badanego ośrodka bez żadnych przerw , rozmieszczonych w sposób ciągły w zajmowanej przez nią przestrzeni . Na tym założeniu opiera się wiele dyscyplin fizycznych, na przykład hydrodynamika, aerodynamika i teoria sprężystości. Matematyczna koncepcja ciągłości naturalnie odgrywa dużą rolę w tych dyscyplinach, podobnie jak w wielu innych.
Rozważmy pewną funkcję \(y=f(x)\) i dobrze zdefiniowaną wartość zmiennej niezależnej \(x_0\) . Jeśli nasza funkcja odzwierciedla jakiś proces ciągły, to wartości \(x\), które niewiele różnią się od \(x_0\), powinny odpowiadać wartościom funkcji \(f(x)\), które niewiele różnią się od wartość \(f(x_0)\) w punkcie \(x_0\) . Zatem jeśli przyrost \(x-x_0\) zmiennej niezależnej jest mały, to odpowiadający mu przyrost \(f(x)-f(x_0)\) funkcji również musi być mały. Innymi słowy, jeśli przyrost zmiennej niezależnej \(x-x_0\) dąży do zera, to przyrost \(f(x)-f(x_0)\) funkcji musi z kolei dążyć do zera, co można zapisać następująco:
\(\lim_(x-x_0\to0)\Bigl=0.\)
Zależność ta jest matematyczną definicją ciągłości funkcji w punkcie \(x_0\).
Funkcja \(f(x)\) nazywana jest ciągłą w punkcie \(x_0\), jeśli spełniona jest równość (1).
Podajmy inną definicję:
Funkcja nazywana jest ciągłą dla wszystkich wartości należących do danego odcinka, jeżeli jest ciągła w każdym punkcie \(x_0\) tego odcinka, tj. w każdym takim punkcie równość (1) jest spełniona.
Zatem, aby wprowadzić matematyczną definicję właściwości funkcji, która polega na tym, że jej wykres jest krzywą ciągłą (w potocznym tego słowa znaczeniu), konieczne stało się w pierwszej kolejności określenie lokalnej, lokalnej właściwości funkcji ciągłość (ciągłość w punkcie \(x_0\) ), a następnie na tej podstawie określić ciągłość funkcji na całym odcinku.
Powyższa definicja, wskazana po raz pierwszy na początku ubiegłego wieku przez Cauchy’ego, jest powszechnie przyjęta we współczesnej analizie matematycznej. Testowanie na licznych konkretnych przykładach wykazało, że ta definicja dobrze odpowiada naszej obecnej praktycznej koncepcji funkcji ciągłej, na przykład idei wykresu ciągłego.
Przykładami funkcji ciągłych są podstawowe funkcje znane ze szkolnej matematyki \(x^n,\) \(\sin(x),\) \(\cos(x),\) \(a^x,\) \ ( \lg(x),\) \(\arcsin(x),\) \(\arccos(x)\) . Wszystkie wymienione funkcje są ciągłe w przedziałach zmian \(x\), w których są zdefiniowane.
Jeśli dodamy, odejmiemy, pomnożymy i podzielimy funkcje ciągłe (z mianownikiem różnym od zera), to w rezultacie ponownie otrzymamy funkcję ciągłą. Jednak podczas dzielenia ciągłość jest zwykle przerywana dla tych wartości \(x_0\), przy których funkcja w mianowniku dąży do zera. Wynik dzielenia reprezentuje wówczas funkcję nieciągłą w punkcie \(x_0\).
Za przykład funkcji nieciągłej w punkcie \(y=0\) może służyć funkcja \(y=\frac(1)(x)\). Szereg innych przykładów funkcji nieciągłych dają wykresy pokazane na ryc. 1.
Zalecamy dokładne przejrzenie tych wykresów. Należy zauważyć, że nieciągłości funkcji są różne: czasami, gdy \(x\) zbliża się do punktu \(x_0\), w którym funkcja ulega nieciągłości, granica \(f(x)\) istnieje, ale różni się od \(f (x_0)\ ), a czasami, jak na ryc. 1c, granica ta po prostu nie istnieje. Zdarza się również, że gdy \(x\) zbliża się do \(x_0\) z jednej strony \(f(x)-f(x_0)\to0\) , a jeśli \(x\do x_0\) zbliża się z drugiej z drugiej strony, wówczas \(f(x)-f(x_0)\) nie dąży już do zera. W tym przypadku mamy oczywiście nieciągłość funkcji, choć można o niej powiedzieć, że w tym momencie jest ona „ciągła z jednej strony”. Wszystkie te przypadki można prześledzić na podanych wykresach.
Definicja ciągłości funkcji
1. Funkcja \(y=f(x)\) jest ciągła w punkcie \(x=a\), jeśli granice po lewej i prawej stronie są równe i równe wartości funkcji w tym punkcie, tj.
\(\lim_(x\do a-0)f(x)=\lim_(x\do a+0)f(x)=f(a).\)
2. Funkcja \(y=f(x)\) jest ciągła w punkcie \(x=a\), jeżeli jest w tym punkcie zdefiniowana i jeżeli nieskończenie małemu przyrostowi argumentu odpowiada nieskończenie małemu przyrostowi funkcji, tj. \(\lim_(\Delta x\do 0)\Delta y=0\) w pobliżu punktu \(a\) .
Suma, różnica i iloczyn skończonej liczby funkcji ciągłych jest funkcją ciągłą.
Funkcja ciągła na przedziale \(\) przyjmuje dowolną wartość pośrednią między jej najmniejszą \(m\) a największą wartością \(M\), to znaczy \(m\leqslant f(x)\leqslant M\) dla wszystkich \(x\in\) . Wynika z tego, że jeżeli na brzegach odcinka \(\) funkcja ma różne znaki, to wewnątrz odcinka istnieje przynajmniej jedna wartość \(x=c\), przy której funkcja zanika. Ta właściwość ciągłości funkcji pozwala znaleźć w przybliżeniu pierwiastki wielomianów.
Punkty przerwania funkcji
Nazywa się wartości argumentów, które nie spełniają warunków ciągłości punkty przerwania funkcji. W tym przypadku wyróżnia się dwa typy punktów nieciągłości funkcji.
Jeżeli dla \(x\to a\) po lewej stronie funkcja ma skończoną granicę \(k_1\) , a dla \(x\to a\) po prawej stronie funkcja ma skończoną granicę \(k_2\) i \(k_1\ne k_2\) , to mówią, że funkcja dla \(x=a\) ma pęknięcie pierwszego rodzaju. Różnica \(|k_1-k_2|\) określa skok funkcji w punkcie \(x=a\) . Wartość funkcji w \(x=a\) może być równa dowolnej liczbie \(k_3\) .
Jeśli wartość funkcji w \(x=a\) jest równa \(k_1\) , to mówimy, że funkcja jest ciągła; jeśli \(k_2\) , to mówią, że funkcja jest prawociągła.
Jeśli \(k_1=k_2\ne k_3\) mówią, że funkcja ma w punkcie \(a\) naprawialna luka.
Jeżeli dla \(x\to a\) po prawej lub lewej stronie granica funkcji nie istnieje lub jest równa nieskończoności, czyli \(\lim_(x\to a)f(x)=\infty \), to mówią, że funkcja for \ (x=a\) ma nieciągłość drugiego rodzaju.
Przykład 1. Znajdź zbiór wartości \(x\), dla którego funkcja \(y=x^3-2x\) jest ciągła.
Rozwiązanie. Znajdźmy przyrost funkcji
\(\Delta y=(x+\Delta x)^3-2(x+\Delta x)-(x^3-2x)=\Delta x\,(\Delta x^2+3x\Delta x+3x^ 2-2).\)
Dla dowolnych wartości zmiennej \(x\) przyrost wynosi \(\Delta y\to0\) chyba że \(\Delta x\to0\) więc funkcja jest ciągła dla wszystkich rzeczywistych wartości zmiennej \ (X\) .
Przykład 2. Udowodnij ciągłość funkcji \(y=\frac(1)(x-1)\) w punkcie \(x=3\) .
Rozwiązanie. Aby to udowodnić, znajdźmy przyrost funkcji \(y\), gdy wartość argumentu przesuwa się z \(x=3\) do \(x=3+\Delta x\)
\(\Delta y=\frac(1)(3+\Delta x-1)-\frac(1)(3-1)=\frac(1)(2+\Delta x)-\frac(1) (2)=\frac(2-2-\Delta x)(2(2+\Delta x))=\frac(-\Delta x)(2(2+\Delta x)).\)
Znajdźmy granicę przyrostu funkcji w \(\Delta x\to0\)
\(\lim_(\Delta x\to0)\Delta y=-\lim_(\Delta x\to0)\frac(\Delta x)(2(2+\Delta x))=-\frac(0)( 2(2+0))=0.\)
Ponieważ granica przyrostu funkcji w \(\Delta x\to0\) jest równa zeru, to funkcja w \(x\to3\) jest ciągła.
Przykład 3. Określ naturę nieciągłości funkcji i skonstruuj wykresy:
\(\mathrm(a))~y=\frac(1)(x-1)~\text(if)~x=1;\qquad\mathrm(b))~y=\frac(x)(| x|)~\text(if)~x=0;\qquad\mathrm(c))~y=\begin(cases)2x,&\text(if)~x\ne2,\\1,&\text (if)~x=2;\end(cases)\qquad\mathrm(d))~y=a^(1/x)~(a>1);\qquad\mathrm(e))~y=\ nazwaoperatora(arctg)\frac(1)(x).\)
Rozwiązanie.
a) Gdy \(x=1\) funkcja nie jest zdefiniowana, w tym miejscu znajdujemy jednostronne granice:
\(\lim_(x\to1-0)\frac(1)(x-1)=-\infty;\quad\lim_(x\to1+0)\frac(1)(x-1)=+\ infty.\)
Zatem w punkcie \(x=1\) funkcja ma nieciągłość drugiego rodzaju.
b) Dla \(x<0\) предел функции равен \(\lim_(0-0)\frac(x)(|x|)=-1=k_1\). Gdy \(x>0\) granica jest równa \(\lim_(0+0)\frac(x)(|x|)=1=k_2\). Zatem w punkcie \(x=1\) funkcja \(y\) ma nieciągłość pierwszego rodzaju, a skok funkcji jest równy \(|k_1-k_2|=|-1-1|= 2\) .
c) Funkcja jest zdefiniowana na całej osi liczbowej, nieelementarnej, ponieważ w punkcie \(x=2\) zmienia się wyrażenie analityczne funkcji. Zbadajmy ciągłość funkcji w punkcie \(x=2\) :
\(\lim_(x\to2-0)=4,\quad\lim_(x\to2+0)2x=4,\quad y(2)=1,\quad k_1=k_2\ne k_3.\)
Jest oczywiste, że w punkcie \(x=2\) funkcja ma usuwalną nieciągłość.
d) Znajdź lewą i prawą granicę funkcji w punkcie \(x=0\) :
\(y(+0)=\lim_(x\to+0)a^(1/x)=+\infty,\quad y(-0)=\lim_(x\to-0)a^(1 /x)=0.\)
Zatem w punkcie \(x=0\) funkcja ma po prawej stronie nieciągłość drugiego rodzaju, a po lewej ciągłość.
e) Znajdź jednostronne granice funkcji w punkcie \(x=0\) :
\(y(+0)=\lim_(x\to+0)\nazwa operatora(arctg)\frac(1)(x)=\frac(\pi)(2),\quad y(-0)=\ lim_(x\to-0)\operatorname(arctg)\frac(1)(x)=-\frac(\pi)(2).\)
Zatem w punkcie \(x=0\) po obu stronach funkcji \(y=\nazwa operatora(arctg)\frac(1)(x)\) wyścigi konne
JavaScript jest wyłączony w Twojej przeglądarce.Aby wykonać obliczenia, musisz włączyć kontrolki ActiveX!
- Co oznacza indywidualność?
- Od czego zależy indywidualność człowieka?
- Zagadnienia tworzenia klastrowego systemu edukacji w Federacji Rosyjskiej
- Testy ujednoliconego egzaminu państwowego w literaturze Co obejmuje literatura ujednoliconego egzaminu państwowego
- Jak zapłacić podatek transportowy dla osób prawnych
- Karta do indywidualnego rozliczania kwot naliczonych wpłat i pozostałych wynagrodzeń oraz kwot naliczonych składek ubezpieczeniowych Karta rocznych składek ubezpieczeniowych
- Błąd podczas wypełniania konturu
- Audyt biurka: zmiany
- Warunki przeprowadzenia eksperymentu rufowego
- Stan systemu i procesy
- Rozwój działalności badawczej studentów Aleksieja Siergiejewicza Obuchowa
- Studia orientalne i afrykańskie
- Yelets State University nazwany na cześć
- Co pokazuje i jak obliczyć wewnętrzną stopę zwrotu?
- Yaroslav Samoilov to specjalista ds. relacji bez wykształcenia zawodowego. Chcesz ratować swój związek?
- Perm Pharmaceutical Academy: recenzje, wydziały
- Trader Dmitrij Czeremuszkin
- Główne zagadnienia gospodarcze
- Konkurs kreatywny: przystępujemy do programów szkoleniowych licencjackich na Wydziale Dziennikarstwa Uniwersytetu Państwowego w Petersburgu
- Zarządzanie nowoczesną szkołą na przykładzie tworzenia klastra edukacyjnego









