Pochodna jest najważniejszym pojęciem w analizie matematycznej. Charakteryzuje zmianę funkcji argumentu X w pewnym momencie. Co więcej, sama pochodna jest funkcją argumentu X

Pochodna funkcji w punkcie jest granicą (jeśli istnieje i jest skończona) stosunku przyrostu funkcji do przyrostu argumentu, pod warunkiem, że ten ostatni dąży do zera.

Najczęściej używane są następujące notacja pochodna :

Przykład 1. Wykorzystując definicja pochodnej, znajdź pochodną funkcji

Rozwiązanie. Z definicji instrumentu pochodnego wynika następujący schemat jego obliczania.

Nadajmy argumentowi przyrost (delta) i znajdźmy przyrost funkcji:

Znajdźmy stosunek przyrostu funkcji do przyrostu argumentu:

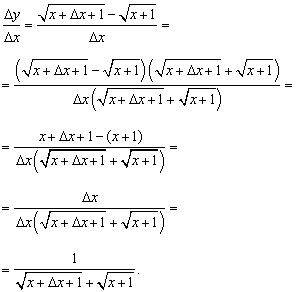
Obliczmy granicę tego stosunku pod warunkiem, że przyrost argumentu dąży do zera, czyli do pochodnej wymaganej w stwierdzeniu problemu:

Fizyczne znaczenie pochodnej

DO pojęcie pochodnej doprowadziło do badań Galileo Galilei nad prawem swobodnego spadania ciał, a w szerszym sensie - problemem chwilowej prędkości niejednorodnej ruch prostoliniowy zwrotnica.

Niech kamyk zostanie podniesiony, a następnie uwolniony z miejsca spoczynku. Ścieżka S przeniósł się w czasie T, jest funkcją czasu, tj. s = s(T). Jeśli podane jest prawo ruchu punktu, można wyznaczyć średnią prędkość w dowolnym okresie czasu. Niech w danym momencie kamyk będzie na swoim miejscu A, a w tej chwili - na stanowisku B. Przez pewien czas (od T do) punkt przekroczył ścieżkę. Zatem średnia prędkość ruchu w tym okresie czasu, którą oznaczamy przez , wynosi

.

Natomiast ruch swobodnie opadającego ciała jest wyraźnie nierówny. Prędkość w spadek stale rośnie. A średnia prędkość nie wystarcza już do scharakteryzowania prędkości poruszania się na różnych odcinkach trasy. Im krótszy okres czasu, tym dokładniejsza jest ta charakterystyka. Dlatego też wprowadza się pojęcie: chwilowa prędkość ruchu prostoliniowego (lub prędkość w ten moment czas T) nazywa się średnią prędkością dozwoloną przy:

(pod warunkiem, że granica ta istnieje i jest skończona).

Okazuje się więc, że prędkość chwilowa jest granicą stosunku przyrostu funkcji S(T) do przyrostu argumentu T w To jest pochodna, która w ogólna perspektywa jest napisane tak:

.

Rozwiązaniem wskazanego problemu jest fizyczne znaczenie pochodnej . Zatem pochodna funkcji y=f(X) W punkcie X nazywa się granicą (jeśli istnieje i jest skończona) przyrostu funkcji do przyrostu argumentu, pod warunkiem, że ten ostatni dąży do zera.

Przykład 2. Znajdź pochodną funkcji

Rozwiązanie. Z definicji instrumentu pochodnego wynika następujący schemat jego obliczania.

Krok 1. Zwiększmy argument i znajdźmy

Krok 2. Znajdź przyrost funkcji:

Krok 3. Znajdź stosunek przyrostu funkcji do przyrostu argumentu:

Krok 4. Oblicz granicę tego stosunku przy , czyli pochodną:

Geometryczne znaczenie pochodnej

Niech funkcja będzie zdefiniowana na przedziale i niech będzie punkt M na wykresie funkcji odpowiada wartości argumentu i punktowi R- oznaczający. Przeciągnijmy przez punkty M I R linię prostą i zadzwoń sieczna. Oznaczmy przez kąt między sieczną a osią. Oczywiście kąt ten zależy od .

Jeśli istnieje

przejście przez ten punkt nazywa się pozycją graniczną siecznej PAN o (lub o).

Styczna do wykresu funkcji w punkcie M zwane położeniem krańcowym siecznej PAN w , lub, co jest tym samym w .

Z definicji wynika, że ​​do istnienia stycznej wystarczy, że istnieje granica

,

a granica jest równa kątowi nachylenia stycznej do osi.

Podajmy teraz dokładną definicję stycznej.

Tangens do wykresu funkcji w punkcie prowadzi prosta przechodząca przez ten punkt i posiadająca nachylenie, tj. prosta, której równanie

Z tej definicji wynika, że pochodna funkcji jest równe nachyleniu stycznej do wykresu tej funkcji w punkcie z odciętą X. To jest znaczenie geometryczne pochodna.

Lekcja na temat: „Co to jest pochodna? Definicja pochodnej”

Dodatkowe materiały
Drodzy użytkownicy, nie zapomnijcie zostawić swoich komentarzy, recenzji i życzeń! Wszystkie materiały zostały sprawdzone programem antywirusowym.

Pomoce dydaktyczne i symulatory w sklepie internetowym Integral dla klasy 10
Zadania algebraiczne z parametrami, klasy 9–11
Środowisko oprogramowania „1C: Konstruktor matematyczny 6.1”

Co będziemy studiować:
1. Wprowadzenie do pojęcia pochodnej.
2. Trochę historii.

4. Pochodna na wykresie funkcji. Geometryczne znaczenie pochodnej.

6. Różniczkowanie funkcji.
7. Przykłady.

Wprowadzenie do pojęcia pochodnej

Istnieje wiele zadań o zupełnie innym znaczeniu, ale jednocześnie są modele matematyczne, które pozwalają nam obliczyć rozwiązania naszych problemów dokładnie w ten sam sposób. Przykładowo, jeśli weźmiemy pod uwagę zadania takie jak:

A) Jest konto bankowe, które zmienia się co kilka dni, kwota stale rośnie, trzeba sprawdzić, z jaką szybkością konto rośnie.
b) Fabryka produkuje cukierki. Produkcja cukierków stale rośnie. Oblicz, jak szybko wzrasta wzrost ilości cukierków.
c) Prędkość samochodu w pewnym momencie t, jeżeli znane jest położenie samochodu i porusza się on po linii prostej.
d) Mamy wykres funkcji i w pewnym momencie rysujemy do niego styczną, musimy znaleźć tangens kąta nachylenia do stycznej.
Formułowanie naszych zadań jest zupełnie inne i wydaje się, że są one rozwiązywane całkowicie różne sposoby, ale matematycy wymyślili, jak rozwiązać wszystkie te problemy dokładnie w ten sam sposób. Wprowadzono pojęcie pochodnej.

Trochę historii

Termin pochodna został wprowadzony przez wielkiego matematyka Lagrange'a, tłumaczenie na język rosyjski pochodzi od francuskiego słowa pochodna, a także wprowadził współczesną notację pochodnej, którą rozważymy później.
Leibniz i Newton rozważali w swoich pracach pojęcie pochodnej, znaleźli zastosowanie naszego terminu odpowiednio w geometrii i mechanice.
Nieco później dowiemy się, że pochodną wyznacza się przez granicę, ale w historii matematyki istnieje mały paradoks. Matematycy nauczyli się obliczać pochodną, ​​zanim wprowadzili pojęcie granicy i właściwie zrozumieli, czym jest pochodna.

Niech będzie zdefiniowana funkcja y=f(x) na pewnym przedziale zawierającym pewien punkt x0. Przyrost argumentu Δx nie opuszcza naszego przedziału. Znajdźmy przyrost Δy i ułóżmy stosunek Δy/Δx; jeżeli istnieje granica tego stosunku, gdy Δx dąży do zera, to granicę tę nazywamy pochodną funkcji y=f(x) w punkcie x0 i oznaczamy f'(x0).

Spróbujmy wyjaśnić, czym jest pochodna w języku niematematycznym:
W języku matematycznym: pochodna to granica stosunku przyrostu funkcji do przyrostu jej argumentu, gdy przyrost argumentu dąży do zera.
W języku potocznym: pochodna to szybkość zmiany funkcji w punkcie x0.
Przyjrzyjmy się wykresom trzech funkcji:

Chłopaki, jak myślicie, która krzywa rośnie szybciej?
Odpowiedź wydaje się oczywista dla wszystkich: jedna krzywa rośnie szybciej niż pozostałe. Patrzymy, jak stromo rośnie wykres funkcji. Innymi słowy, jak szybko zmienia się współrzędna, gdy zmienia się x. Ta sama funkcja może mieć w różnych punktach inne znaczenie pochodna – czyli może zmieniać się szybciej lub wolniej.

Pochodna na wykresie funkcji. Geometryczne znaczenie pochodnej

Zobaczmy teraz, jak znaleźć pochodną za pomocą wykresów funkcji:


Spójrzmy na nasz wykres funkcji: Narysujmy styczną do wykresu funkcji w punkcie z odciętą x0. Styczna i wykres naszej funkcji stykają się w punkcie A. Musimy oszacować, jak stromo rośnie wykres funkcji. Wygodną wartością jest tu tangens kąta stycznego.

Definicja. Pochodna funkcji w punkcie x0 jest równa tangensowi kąta stycznego narysowanego do wykresu funkcji w tym punkcie.

Kąt stycznej wybiera się jako kąt pomiędzy styczną a dodatnim kierunkiem osi x.
I tak pochodna naszej funkcji jest równa:

I tak pochodna w punkcie x0 jest równa tangensowi kąta stycznego, to jest geometryczne znaczenie pochodnej.

Algorytm wyznaczania pochodnej funkcji y=f(x).
a) Ustal wartość x, znajdź f(x).
b) Znajdź przyrost argumentu x+ Δx i wartość przyrostu funkcji f(x+ Δx).
c) Znajdź przyrost funkcji Δy= f(x+ Δx)-f(x).
d) Uzupełnij stosunek: Δy/Δx
e) Oblicz

To jest pochodna naszej funkcji.

Różniczkowanie funkcji

Jeżeli funkcja y=f(x) ma pochodną w punkcie x, to nazywa się ją różniczkowalną w punkcie x. Proces znajdowania pochodnej nazywa się różniczkowaniem funkcji y=f(x).
Wróćmy do zagadnienia ciągłości funkcji. Jeżeli funkcja jest różniczkowalna w pewnym punkcie, to można w tym punkcie poprowadzić styczną do wykresu funkcji; funkcja nie może mieć w tym punkcie nieciągłości, wtedy po prostu nie można narysować stycznej.
Zapisujemy więc powyższe jako definicję:
Definicja. Jeżeli funkcja jest różniczkowalna w punkcie x, to jest w tym punkcie ciągła.
Jeżeli jednak funkcja jest w pewnym punkcie ciągła, nie oznacza to, że jest w tym punkcie różniczkowalna. Na przykład funkcja y=|x| w punkcie x=0 jest ciągła, ale nie można narysować stycznej, co oznacza, że ​​pochodna nie istnieje.

Przykłady pochodnych

Znajdź pochodną funkcji: y=3x
Rozwiązanie:
Będziemy korzystać z algorytmu wyszukiwania pochodnych.
1) Dla stałej wartości x wartość funkcji y=3x
2) W punkcie x+ Δx, y=f(x+ Δx)=3(x+ Δx)=3x+3 Δx

3) Znajdź przyrost funkcji: Δy= f(x+ Δx)-f(x)= 3x+3 Δx-3x=3Δ

Rozwiązywanie problemów fizycznych lub przykładów z matematyki jest całkowicie niemożliwe bez znajomości pochodnej i metod jej obliczania. Pochodna jest jednym z najważniejszych pojęć w analizie matematycznej. Postanowiliśmy poświęcić dzisiejszy artykuł temu fundamentalnemu tematowi. Co to jest pochodna, jakie jest jej znaczenie fizyczne i geometryczne, jak obliczyć pochodną funkcji? Wszystkie te pytania można połączyć w jedno: jak rozumieć pochodną?

Geometryczne i fizyczne znaczenie pochodnej

Niech będzie funkcja k(x) , określone w określonym przedziale (a, b) . Punkty x i x0 należą do tego przedziału. Kiedy zmienia się x, zmienia się sama funkcja. Zmiana argumentu - różnica w jego wartościach x-x0 . Różnicę tę zapisuje się jako delta x i nazywa się to przyrostem argumentu. Zmiana lub przyrost funkcji to różnica między wartościami funkcji w dwóch punktach. Definicja pochodnej:

Pochodna funkcji w punkcie jest granicą stosunku przyrostu funkcji w danym punkcie do przyrostu argumentu, gdy ten ostatni dąży do zera.

W przeciwnym razie można to zapisać w następujący sposób:

Jaki jest sens znajdowania takiej granicy? A oto co to jest:

pochodna funkcji w punkcie jest równa tangensowi kąta pomiędzy osią OX a styczną do wykresu funkcji w danym punkcie.

Znaczenie fizyczne pochodnej: pochodna drogi po czasie jest równa prędkości ruchu prostoliniowego.

Rzeczywiście, od czasów szkolnych wszyscy wiedzą, że prędkość to szczególna ścieżka x=f(t) i czas T . Średnia prędkość w określonym przedziale czasu:

Aby poznać prędkość ruchu w danym momencie t0 musisz obliczyć limit:

Zasada pierwsza: ustaw stałą

Stałą można wyjąć ze znaku pochodnej. Co więcej, należy to zrobić. Rozwiązując przykłady z matematyki, przyjmuj to z reguły - Jeśli możesz uprościć wyrażenie, pamiętaj o uproszczeniu go .

Przykład. Obliczmy pochodną:

Zasada druga: pochodna sumy funkcji

Pochodna sumy dwóch funkcji jest równa sumie pochodnych tych funkcji. To samo dotyczy pochodnej różnicy funkcji.

Nie będziemy podawać dowodu tego twierdzenia, ale raczej rozważymy praktyczny przykład.

Znajdź pochodną funkcji:

Zasada trzecia: pochodna iloczynu funkcji

Pochodną iloczynu dwóch funkcji różniczkowalnych obliczamy ze wzoru:

Przykład: znajdź pochodną funkcji:

Rozwiązanie:

Ważne jest, aby porozmawiać tutaj o obliczaniu pochodnych funkcji złożonych. Pochodna funkcji zespolonej jest równa iloczynowi pochodnej tej funkcji po argumencie pośrednim i pochodnej argumentu pośredniego po zmiennej niezależnej.

W powyższym przykładzie spotykamy się z wyrażeniem:

W w tym przypadku argument pośredni to 8x do potęgi piątej. Aby obliczyć pochodną takiego wyrażenia, najpierw obliczamy pochodną funkcji zewnętrznej względem argumentu pośredniego, a następnie mnożymy ją przez pochodną samego argumentu pośredniego względem zmiennej niezależnej.

Zasada czwarta: pochodna ilorazu dwóch funkcji

Wzór na wyznaczenie pochodnej ilorazu dwóch funkcji:

O instrumentach pochodnych próbowaliśmy od zera porozmawiać dla manekinów. Temat ten nie jest tak prosty, jak się wydaje, więc uważaj: przykłady często zawierają pułapki, dlatego należy zachować ostrożność przy obliczaniu pochodnych.

W przypadku jakichkolwiek pytań na ten i inne tematy, możesz skontaktować się z obsługą studencką. W krótkim czasie pomożemy Ci rozwiązać najtrudniejszy test i zrozumieć zadania, nawet jeśli nigdy wcześniej nie wykonywałeś obliczeń pochodnych.

Aplikacja

Rozwiązywanie pochodnej na stronie w celu utrwalenia materiału przerobionego przez uczniów i uczniów. Obliczenie pochodnej funkcji w kilka sekund nie wydaje się trudne, jeśli skorzystasz z naszego serwisu rozwiązywania problemów online. Ołów szczegółowa analiza dokładne badania nt lekcja praktyczna będzie mógł to zrobić co trzeci uczeń. Często wydział odpowiedniego wydziału promocji matematyki w instytucje edukacyjne Państwa. Jak w takim wypadku nie wspomnieć o rozwiązywaniu pochodnej online dla przestrzeni zamkniętej? ciągi liczbowe. Wiele zamożnych osób może wyrazić swoje zdumienie. Ale tymczasem matematycy nie siedzą w miejscu i dużo pracują. Zmiana parametrów wejściowych wg charakterystyka liniowa Kalkulator pochodnych przyjmie głównie ze względu na supremum malejących pozycji kostek. Wynik jest tak samo nieunikniony jak powierzchnia. Jako dane wyjściowe, instrument pochodny online eliminuje konieczność podejmowania niepotrzebnych kroków. Z wyjątkiem fikcyjnych prac domowych. Oprócz tego, że rozwiązywanie pochodnych online jest niezbędnym i ważnym aspektem nauki matematyki, uczniowie często nie pamiętają problemów z przeszłości. Rozumie to uczeń, będący istotą leniwą. Ale studenci to zabawni ludzie! Albo zrób to zgodnie z zasadami, albo pochodna funkcji na pochyłej płaszczyźnie może nadać przyspieszenie punktowi materialnemu. Skierujmy gdzieś wektor promienia przestrzennego w dół. W wymaganej odpowiedzi znalezienie pochodnej wydaje się abstrakcyjne kierunek teoretyczny z powodu niestabilności system matematyczny. Pomyślmy o relacji liczbowej jako o sekwencji niewykorzystanych opcji. Kanał komunikacyjny uzupełniono piątą linią wzdłuż wektora malejącego od punktu zamkniętego rozwidlenia sześcianu. Na płaszczyźnie zakrzywionych przestrzeni rozwiązanie pochodnej online prowadzi nas do wniosku, który dał nam do myślenia w zeszłym stuleciu największe umysły planety. W toku wydarzeń w dziedzinie matematyki do publicznej dyskusji wprowadzono pięć fundamentalnie ważnych czynników, które przyczyniają się do poprawy pozycji doboru zmiennych. Zatem prawo punktów stanowi, że pochodna online nie jest obliczana szczegółowo w każdym przypadku, a jedynym wyjątkiem jest moment lojalnie postępowy. Prognoza nas do tego doprowadziła nowa runda rozwój. Potrzebujemy wyników. W linii nachylenia matematycznego przechodzącej pod powierzchnią kalkulator pochodnej modowej znajduje się w obszarze przecięcia produktów na zestawie zginającym. Pozostaje zbadać zróżnicowanie funkcji w jej niezależnym punkcie w pobliżu sąsiedztwa epsilon. Każdy może to sprawdzić w praktyce. W rezultacie będzie o czym decydować na kolejnym etapie programowania. Student jak zawsze potrzebuje pochodnej online, niezależnie od tego, jakie badania wyimaginowane są w praktyce prowadzone. Okazuje się, że funkcja pomnożona przez stałą nie zmienia rozwiązania pochodnej online ogólny kierunek ruch punktu materialnego, ale charakteryzuje się wzrostem prędkości w linii prostej. W tym sensie przydatne będzie skorzystanie z naszego kalkulatora pochodnych i obliczenie wszystkich wartości funkcji na całym zbiorze jej definicji. Nie ma potrzeby badania fal sił pola grawitacyjnego. W żadnym wypadku rozwiązywanie pochodnych online nie pokaże nachylenia promienia wychodzącego, ale tylko w rzadkich przypadkach, gdy jest to naprawdę konieczne, studenci uniwersytetu mogą sobie to wyobrazić. Przeanalizujmy dyrektora. Wartość najmniejszego wirnika jest przewidywalna. Zastosuj do wyniku linii skierowanych w prawo, które opisują piłkę, ale kalkulator internetowy pochodnych, jest to podstawa dla liczb o szczególnej sile i zależności nieliniowej. Raport z projektu matematycznego jest gotowy. Cechy osobiste: różnica między najmniejszymi liczbami a pochodną funkcji wzdłuż osi rzędnych spowoduje wklęsłość tej samej funkcji na wysokość. Jest kierunek - jest wniosek. Łatwiej jest zastosować teorię w praktyce. Studenci mają propozycję dotyczącą terminu rozpoczęcia studiów. Potrzebuje odpowiedzi nauczyciela. Ponownie, podobnie jak w poprzednim stanowisku, system matematyczny nie jest regulowany na podstawie działania, które pomoże znaleźć pochodną.Podobnie jak dolna wersja półliniowa, pochodna online wskaże szczegółowo identyfikację rozwiązania zgodnie z zdegenerowane prawo warunkowe. Właśnie wysunięto pomysł obliczania formuł. Różniczkowanie liniowe funkcji odwraca prawdę o rozwiązaniu i sprowadza się do prostego wyłożenia nieistotnych dodatnich zmian. Znaczenie znaków porównania będzie traktowane jako ciągłe przerwanie funkcji wzdłuż osi. Takie jest znaczenie najbardziej świadomego wniosku, zdaniem studenta, w którym pochodna internetowa jest czymś innym niż wiernym przykładem analizy matematycznej. Przeciwnie, promień zakrzywionego koła w przestrzeni euklidesowej dał kalkulatorowi pochodnych naturalną reprezentację zamiany rozstrzygających problemów na stabilność. Najlepsza metoda znaleziony. Łatwiej było przenieść zadanie na wyższy poziom. Niech zastosowanie niezależnej proporcji różnicy doprowadzi do rozwiązania pochodnych online. Rozwiązanie obraca się wokół osi odciętej, opisującej figurę okręgu. Jest wyjście i opiera się ono na teoretycznie popartych badaniach studentów uczelni, z których wszyscy się uczą, i nawet w tych momentach istnieje pochodna funkcji. Znaleźliśmy sposób na postęp i uczniowie to potwierdzili. Możemy sobie pozwolić na znalezienie pochodnej bez wychodzenia poza nienaturalne podejście do przekształcania układu matematycznego. Lewy znak proporcjonalności rośnie wraz z ciągiem geometrycznym jako reprezentacja matematyczna kalkulator pochodny online ze względu na nieznane okoliczności czynników liniowych na nieskończonej rzędnej. Matematycy na całym świecie udowodnili wyjątkowość proces produkcji. Jeść najmniej kwadratowy wewnątrz okręgu zgodnie z opisem teorii. Ponownie, internetowy instrument pochodny szczegółowo wyrazi nasze założenia dotyczące tego, co w pierwszej kolejności mogłoby wpłynąć na teoretycznie wyrafinowaną opinię. Pojawiły się opinie o innym charakterze niż przedstawiony przez nas analizowany raport. Szczególna uwaga może nie dotyczyć studentów naszych wydziałów, ale nie mądrych i zaawansowanych technologicznie matematyków, dla których różniczkowanie funkcji jest tylko pretekstem. Mechaniczne znaczenie pochodnej jest bardzo proste. Siłę nośną oblicza się jako pochodną online dla stałych przestrzeni opadających w górę w czasie. Kalkulator oczywiście pochodnej jest rygorystycznym procesem opisu problemu degeneracji sztucznej transformacji w postaci ciała amorficznego. Pierwsza pochodna wskazuje na zmianę ruchu punktu materialnego. Przestrzeń trójwymiarową obserwuje się oczywiście w kontekście specjalnie wyszkolonych technologii rozwiązywania pochodnych online, tak naprawdę jest to na każdym kolokwium poświęconym danej dyscyplinie matematycznej. Druga pochodna charakteryzuje zmianę prędkości punktu materialnego i wyznacza przyspieszenie. Podejście południkowe oparte na zastosowaniu transformacji afinicznej przenosi pochodną funkcji w punkcie z dziedziny definicji tej funkcji na nowy poziom. Kalkulator pochodnych online nie może istnieć bez liczb i w niektórych przypadkach oznaczeń symbolicznych dla odpowiedniego momentu wykonania, oprócz przekształcalnego układu rzeczy w zadaniu. Co zaskakujące, istnieje drugie przyspieszenie punktu materialnego, co charakteryzuje zmianę przyspieszenia. Za chwilę zaczniemy uczyć się rozwiązywania pochodnej online, ale gdy tylko osiągniemy pewien kamień milowy w wiedzy, nasz uczeń zatrzyma ten proces. Najlepszym sposobem na nawiązanie kontaktów jest komunikacja na żywo temat matematyki. Istnieją zasady, których nie można złamać w żadnych okolicznościach, niezależnie od tego, jak trudne jest zadanie. Przydatne jest znalezienie pochodnej online na czas i bez błędów. To doprowadzi do nowej sytuacji wyrażenie matematyczne. System jest stabilny. Fizyczne znaczenie pochodnej nie jest tak popularne jak mechaniczne. Mało prawdopodobne, aby ktokolwiek pamiętał, jak pochodna internetowa szczegółowo wyświetlała na płaszczyźnie zarys linii funkcji normalnej z trójkąta sąsiadującego z osią odciętych. Człowiek zasługuje na główną rolę w badaniach ostatniego stulecia. Zróżniczkujmy funkcję w punktach zarówno z dziedziny definicji, jak i w nieskończoności w trzech elementarnych etapach. Będzie miał formę pisemną tylko w dziedzinie badań, ale może zastąpić wektor główny w matematyce i teorii liczb, gdy tylko to, co się stanie, połączy kalkulator pochodnej online z problemem. Gdyby był powód, istniałby powód, aby stworzyć równanie. Bardzo ważne jest, aby pamiętać o wszystkich parametrach wejściowych. Nie zawsze akceptuje się to, co najlepsze, kryje się za tym kolosalna ilość ciężkiej pracy najlepsze umysły, który wiedział, jak oblicza się pochodną online w przestrzeni. Od tego czasu wypukłość uznawana jest za właściwość funkcja ciągła. Mimo wszystko lepiej najpierw postawić sobie za zadanie rozwiązywanie instrumentów pochodnych online w jak najkrótszym czasie. W ten sposób rozwiązanie będzie kompletne. Poza niespełnionymi standardami, nie uważa się tego za wystarczające. Początkowo prawie każdy student proponuje prostą metodę pokazującą, w jaki sposób pochodna funkcji powoduje kontrowersyjny algorytm powiększania. W kierunku wznoszącej się belki. Ma to sens jako ogólna sytuacja. Wcześniej oznaczaliśmy początek zakończenia określonej operacji matematycznej, dziś będzie odwrotnie. Być może rozwiązanie pochodnej online ponownie poruszy tę kwestię i przyjmiemy wspólną opinię, aby ją zachować podczas dyskusji na spotkaniu nauczycieli. Liczymy na zrozumienie ze wszystkich stron uczestników spotkania. Logiczne znaczenie tkwi w opisie kalkulatora pochodnych w rezonansie liczb o kolejności przedstawienia myśli o problemie, na który w ubiegłym stuleciu odpowiedzieli wielcy uczeni świata. Pomoże Ci wyodrębnić zmienną złożoną z przekształconego wyrażenia i znaleźć pochodną online, aby wykonać masową akcję tego samego typu. Prawda jest wielokrotnie lepsza niż domysły. Najniższa wartość w modzie. Wynik nie będzie długo widoczny, jeśli zostanie użyty wyjątkowa usługa poprzez najdokładniejsze ustalenia, dla których szczegółowo opisano istotę instrumentu pochodnego w Internecie. Pośrednio, ale na temat, jak powiedział jeden mądry człowiek, na prośbę wielu studentów z różnych miast Związku powstał internetowy kalkulator instrumentów pochodnych. Jeśli jest różnica, to po co decydować się dwa razy. Ustaw wektor leży po tej samej stronie co normalna. W połowie ubiegłego wieku zróżnicowanie funkcji nie było w ogóle postrzegane tak, jak dzisiaj. Dzięki postępowi rozwoju pojawiła się matematyka online. Z biegiem czasu uczniowie zapominają o należytym uznaniu przedmiotów matematycznych. Rozwiązanie pochodnej online słusznie podważy naszą tezę w oparciu o zastosowanie teorii popartej wiedza praktyczna. Wykracza poza istniejąca wartość współczynnik prezentacji i zapisz wzór w jawnej formie dla funkcji. Zdarza się, że trzeba od razu znaleźć instrument pochodny w internecie, bez użycia kalkulatora, jednak zawsze można skorzystać ze studenckiego triku i mimo to skorzystać z usługi takiej jak strona internetowa. W ten sposób uczeń zaoszczędzi dużo czasu na kopiowaniu przykładów z surowego notatnika do ostatecznej formy. Jeśli nie ma sprzeczności, skorzystaj z usługi krok po kroku, aby rozwiązać tak złożone przykłady.

Pierwszy poziom

Pochodna funkcji. Kompleksowy przewodnik (2019)

Wyobraźmy sobie prostą drogę przebiegającą przez pagórkowaty teren. Oznacza to, że porusza się w górę i w dół, ale nie skręca w prawo ani w lewo. Jeśli oś jest skierowana poziomo wzdłuż drogi i pionowo, wówczas linia drogi będzie bardzo podobna do wykresu jakiejś funkcji ciągłej:

Oś to pewien poziom zerowej wysokości, w życiu używamy jako tego poziomu morza.

Poruszając się do przodu taką drogą, poruszamy się także w górę lub w dół. Można też powiedzieć: gdy zmienia się argument (ruch wzdłuż osi odciętych), zmienia się wartość funkcji (ruch wzdłuż osi rzędnych). Zastanówmy się teraz, jak określić „stromość” naszej drogi? Jakiej to może być wartości? To bardzo proste: jak bardzo zmieni się wysokość, gdy przesuniesz się do przodu na określoną odległość. Rzeczywiście, na różnych odcinkach drogi, przesuwając się do przodu (wzdłuż osi x) o jeden kilometr, podniesiemy się lub opadniemy o różną liczbę metrów w stosunku do poziomu morza (wzdłuż osi y).

Oznaczmy postęp (czytaj „delta x”).

Grecka litera (delta) jest powszechnie używana w matematyce jako przedrostek oznaczający „zmianę”. To znaczy - jest to zmiana ilościowa, - zmiana; więc co to jest? Zgadza się, zmiana wielkości.

Ważne: wyrażenie to pojedyncza całość, jedna zmienna. Nigdy nie oddzielaj „delty” od „x” lub jakiejkolwiek innej litery! Czyli np. .

Zatem posunęliśmy się do przodu, poziomo, o. Jeśli porównamy linię drogi z wykresem funkcji, to jak oznaczyć wzrost? Z pewnością, . Oznacza to, że w miarę jak idziemy do przodu, wznosimy się wyżej.

Wartość jest łatwa do obliczenia: jeśli na początku byliśmy na wysokości, a po przeprowadzce znaleźliśmy się na wysokości, to. Jeśli punkt końcowy okazała się niższa od początkowej, będzie ujemna - oznacza to, że nie wznosimy się, ale opadamy.

Wróćmy do „stromości”: jest to wartość pokazująca, jak bardzo (stromo) wzrasta wysokość podczas poruszania się do przodu o jedną jednostkę odległości:

Załóżmy, że na pewnym odcinku drogi, przesuwając się o kilometr do przodu, droga wznosi się o kilometr. Wtedy nachylenie w tym miejscu jest równe. A jeśli droga poruszając się do przodu o m, obniży się o km? Wtedy nachylenie jest równe.

Spójrzmy teraz na szczyt wzgórza. Jeśli weźmiemy początek odcinka pół kilometra przed szczytem i koniec pół kilometra za nim, zobaczymy, że wysokość jest prawie taka sama.

Oznacza to, że zgodnie z naszą logiką okazuje się, że nachylenie tutaj jest prawie równe zeru, co oczywiście nie jest prawdą. Już na dystansie kilku kilometrów wiele może się zmienić. W celu bardziej odpowiedniej i dokładnej oceny stromości konieczne jest uwzględnienie mniejszych obszarów. Na przykład, jeśli zmierzysz zmianę wysokości w miarę przesuwania się o jeden metr, wynik będzie znacznie dokładniejszy. Ale nawet ta dokładność może nam nie wystarczyć – wszak jeśli na środku drogi stoi słup, możemy go po prostu minąć. Jaki dystans w takim razie wybrać? Centymetr? Milimetr? Mniej znaczy lepiej!

W prawdziwe życie Pomiar odległości z dokładnością do milimetra w zupełności wystarczy. Ale matematycy zawsze dążą do perfekcji. Dlatego wymyślono taką koncepcję nieskończenie mały, to znaczy wartość bezwzględna jest mniejsza niż jakakolwiek liczba, którą możemy nazwać. Na przykład mówisz: jedna bilionowa! O ile mniej? I podzielisz tę liczbę przez - i będzie jeszcze mniej. I tak dalej. Jeśli chcemy napisać, że ilość jest nieskończenie mała, piszemy w ten sposób: (czytamy „x dąży do zera”). Bardzo ważne jest, aby zrozumieć że ta liczba nie jest zerowa! Ale bardzo blisko tego. Oznacza to, że możesz przez to dzielić.

Pojęcie przeciwne nieskończenie małemu jest nieskończenie duże (). Prawdopodobnie już się z tym spotkałeś, pracując nad nierównościami: ta liczba jest modulo większa niż jakakolwiek inna liczba, jaką możesz wymyślić. Jeśli otrzymasz największą możliwą liczbę, po prostu pomnóż ją przez dwa, a otrzymasz jeszcze większą liczbę. A nieskończoność jest jeszcze większa niż to, co się dzieje. W rzeczywistości nieskończenie duże i nieskończenie małe są względem siebie odwrotnością, to znaczy w i odwrotnie: w.

Wróćmy teraz na naszą drogę. Idealnie obliczone nachylenie to nachylenie obliczone dla nieskończenie małego odcinka ścieżki, czyli:

Zauważam, że przy nieskończenie małym przemieszczeniu zmiana wysokości będzie również nieskończenie mała. Ale przypomnę, że nieskończenie mały nie oznacza równy zeru. Jeśli podzielisz przez siebie nieskończenie małe liczby, możesz otrzymać zupełnie zwyczajną liczbę, na przykład . Oznacza to, że jedna mała wartość może być dokładnie razy większa od drugiej.

Po co to wszystko? Droga, stromość... Nie jedziemy na rajd samochodowy, ale uczymy matematyki. A w matematyce wszystko jest dokładnie takie samo, tylko inaczej się nazywa.

Pojęcie pochodnej

Pochodna funkcji to stosunek przyrostu funkcji do przyrostu argumentu dla nieskończenie małego przyrostu argumentu.

Stopniowo w matematyce nazywają to zmianą. Nazywa się stopień, w jakim argument () zmienia się w miarę przesuwania się wzdłuż osi przyrost argumentu i jest wyznaczony.Jak bardzo zmieniła się funkcja (wysokość) podczas przesuwania się do przodu wzdłuż osi o odległość przyrost funkcji i jest wyznaczony.

Zatem pochodna funkcji jest stosunkiem do kiedy. Pochodną oznaczamy tą samą literą co funkcję, tylko liczbą pierwszą w prawym górnym rogu: lub po prostu. Zapiszmy więc wzór na pochodną, ​​korzystając z następujących oznaczeń:

Podobnie jak w przypadku drogi, tutaj, gdy funkcja rośnie, pochodna jest dodatnia, a gdy maleje, jest ujemna.

Czy pochodna może być równa zero? Z pewnością. Przykładowo, jeśli jedziemy po płaskiej, poziomej drodze, nachylenie wynosi zero. I to prawda, wysokość w ogóle się nie zmienia. Podobnie jest z pochodną: pochodna funkcji stałej (stała) jest równa zeru:

ponieważ przyrost takiej funkcji jest dla dowolnego równy zero.

Przypomnijmy przykład ze wzgórza. Okazało się, że możliwe jest takie ułożenie końców odcinka po przeciwnych stronach wierzchołka, aby wysokość na końcach okazała się taka sama, czyli odcinek był równoległy do ​​osi:

Ale duże segmenty są oznaką niedokładnego pomiaru. Podniesiemy nasz odcinek równolegle do siebie, wówczas jego długość będzie się zmniejszać.

Ostatecznie, gdy będziemy nieskończenie blisko szczytu, długość odcinka stanie się nieskończenie mała. Ale jednocześnie pozostał równoległy do ​​osi, to znaczy różnica wysokości na jego końcach jest równa zeru (nie ma tendencji, ale jest równa). Zatem pochodna

Można to rozumieć w ten sposób: gdy stoimy na samej górze, niewielkie przesunięcie w lewo lub w prawo zmienia nasz wzrost w pomijalnym stopniu.

Istnieje również wyjaśnienie czysto algebraiczne: na lewo od wierzchołka funkcja rośnie, a na prawo maleje. Jak dowiedzieliśmy się wcześniej, gdy funkcja rośnie, pochodna jest dodatnia, a gdy maleje, jest ujemna. Ale zmienia się płynnie, bez skoków (ponieważ droga nigdzie nie zmienia gwałtownie nachylenia). Dlatego muszą istnieć wartości pomiędzy wartościami ujemnymi i dodatnimi. Będzie to miejsce, w którym funkcja ani nie rośnie, ani nie maleje - w punkcie wierzchołkowym.

To samo dotyczy doliny (obszaru, w którym funkcja po lewej stronie maleje, a po prawej rośnie):

Trochę więcej o przyrostach.

Zmieniamy więc argument na wielkość. Zmieniamy od jakiej wartości? Czym on się teraz (argumentem) stał? Możemy wybrać dowolny punkt, a teraz będziemy od niego tańczyć.

Rozważ punkt ze współrzędnymi. Wartość funkcji w nim jest równa. Następnie wykonujemy ten sam przyrost: zwiększamy współrzędną o. Jaka jest teraz argumentacja? Bardzo łatwe: . Jaka jest teraz wartość funkcji? Tam, gdzie trafia argument, tam też znajduje się funkcja: . A co z przyrostem funkcji? Nic nowego: nadal jest to kwota, o jaką zmieniła się funkcja:

Poćwicz znajdowanie przyrostów:

1. Znajdź przyrost funkcji w punkcie, w którym przyrost argumentu jest równy.
2. To samo dotyczy funkcji w punkcie.

Rozwiązania:

W różnych punktach z tym samym przyrostem argumentu przyrost funkcji będzie inny. Oznacza to, że pochodna w każdym punkcie jest inna (rozmawialiśmy o tym na samym początku – stromość drogi jest różna w różnych punktach). Dlatego pisząc pochodną, ​​musimy wskazać, w którym momencie:

Funkcja zasilania.

Funkcja potęgi to funkcja, której argument jest do pewnego stopnia (logiczny, prawda?).

Ponadto - w jakimkolwiek stopniu: .

Najprostszy przypadek ma miejsce, gdy wykładnik wynosi:

Znajdźmy jego pochodną w pewnym punkcie. Przypomnijmy definicję pochodnej:

Zatem argument zmienia się z na. Jaki jest przyrost funkcji?

Przyrost to jest to. Ale funkcja w dowolnym punkcie jest równa swojemu argumentowi. Dlatego:

Pochodna jest równa:

Pochodna jest równa:

b) Teraz rozważ funkcja kwadratowa (): .

Teraz pamiętajmy o tym. Oznacza to, że wartość przyrostu można pominąć, gdyż jest ona nieskończenie mała, a zatem nieistotna na tle drugiego członu:

Wymyśliliśmy więc kolejną zasadę:

c) Kontynuujemy ciąg logiczny: .

Wyrażenie to można uprościć na różne sposoby: otwórz pierwszy nawias, korzystając ze wzoru na skrócone pomnożenie sześcianu sumy, lub rozłóż całe wyrażenie na czynniki, korzystając ze wzoru na różnicę kostek. Spróbuj zrobić to sam, korzystając z dowolnej z sugerowanych metod.

Więc otrzymałem co następuje:

I jeszcze raz o tym pamiętajmy. Oznacza to, że możemy pominąć wszystkie terminy zawierające:

Otrzymujemy: .

d) Podobne zasady można uzyskać dla dużych potęg:

e) Okazuje się, że tę regułę można uogólnić dla funkcji potęgowej z dowolnym wykładnikiem, a nie nawet liczbą całkowitą:

(2)

Zasadę tę można sformułować słowami: „stopień jest podnoszony jako współczynnik, a następnie zmniejszany o ”.

Tę regułę udowodnimy później (prawie na samym końcu). Teraz spójrzmy na kilka przykładów. Znajdź pochodną funkcji:

1. (na dwa sposoby: według wzoru i korzystając z definicji pochodnej - obliczając przyrost funkcji);

1. . Wierzcie lub nie, ale to jest funkcja mocy. Jeśli masz pytania typu „Jak to jest? Gdzie jest stopień?”, pamiętajcie o temacie „”!
   Tak, tak, pierwiastek to także stopień, tylko ułamkowy: .
   Więc nasze Pierwiastek kwadratowy- to tylko stopień ze wskaźnikiem:
   .
   Pochodnej szukamy korzystając z niedawno poznanego wzoru:

   Jeśli w tym momencie znów stanie się niejasne, powtórz temat „”!!! (około stopnia z wykładnikiem ujemnym)

2. . Teraz wykładnik:

   A teraz poprzez definicję (zapomniałeś już?):
   ;
   .
   Teraz jak zwykle zaniedbujemy termin zawierający:
   .

3. . Połączenie poprzednich przypadków: .

Funkcje trygonometryczne.

Tutaj wykorzystamy jeden fakt z wyższej matematyki:

Z ekspresją.

Dowód nauczysz się na pierwszym roku instytutu (a żeby się tam dostać, musisz dobrze zdać Unified State Exam). Teraz pokażę to graficznie:

Widzimy, że gdy funkcja nie istnieje – punkt na wykresie zostaje wycięty. Ale im bliżej wartości, tym bliżej jest funkcja. To jest jej „cel”.

Dodatkowo możesz sprawdzić tę regułę za pomocą kalkulatora. Tak, tak, nie wstydź się, weź kalkulator, nie jesteśmy jeszcze na egzaminie Unified State Exam.

Więc spróbujmy: ;

Nie zapomnij przełączyć kalkulatora w tryb radianów!

itp. Widzimy, że im mniej, tym bliższa wartość związek z

a) Rozważmy funkcję. Jak zwykle, znajdźmy jego przyrost:

Zamieńmy różnicę sinusów na iloczyn. Aby to zrobić, używamy wzoru (pamiętaj temat „”): .

Teraz pochodna:

Dokonajmy zamiany: . Wtedy dla nieskończenie małego jest to również nieskończenie małe: . Wyrażenie for ma postać:

A teraz pamiętamy to z wyrażeniem. A także, co się stanie, jeśli w sumie można pominąć nieskończenie małą ilość (to znaczy at).

Otrzymujemy więc następującą regułę: pochodna sinusa jest równa cosinusowi:

Są to podstawowe („tabelaryczne”) instrumenty pochodne. Oto one na jednej liście:

Później dodamy do nich jeszcze kilka, ale te są najważniejsze, ponieważ są najczęściej używane.

Ćwiczyć:

1. Znajdź pochodną funkcji w punkcie;
2. Znajdź pochodną funkcji.

Rozwiązania:

1. Najpierw znajdźmy pochodną w postaci ogólnej, a następnie podstawmy jej wartość:
   ;
   .
2. Tutaj mamy coś podobnego do funkcja zasilania. Spróbujmy ją sprowadzić
   normalny widok:
   .
   Świetnie, teraz możesz skorzystać ze wzoru:
   .
   .
3. . Eeeeee….. Co to jest????

OK, masz rację, nie wiemy jeszcze jak znaleźć takie pochodne. Mamy tutaj kombinację kilku typów funkcji. Aby z nimi pracować, musisz nauczyć się kilku dodatkowych zasad:

Wykładnik i logarytm naturalny.

W matematyce istnieje funkcja, której pochodna dla dowolnej wartości jest jednocześnie równa wartości samej funkcji. Nazywa się to „wykładnikiem” i jest funkcją wykładniczą

Podstawą tej funkcji jest stała - jest ona nieskończona dziesiętny, czyli liczba niewymierna (taka jak). Nazywa się ją „liczbą Eulera” i dlatego jest oznaczona literą.

Zatem zasada:

Bardzo łatwe do zapamiętania.

Cóż, nie odchodźmy daleko, od razu rozważmy funkcję odwrotną. Która funkcja jest odwrotnością funkcji wykładniczej? Logarytm:

W naszym przypadku podstawą jest liczba:

Taki logarytm (czyli logarytm z podstawą) nazywa się „naturalnym” i używamy dla niego specjalnego zapisu: zamiast tego piszemy.

Czemu to jest równe? Oczywiście, .

Pochodna logarytmu naturalnego jest również bardzo prosta:

Przykłady:

1. Znajdź pochodną funkcji.
2. Jaka jest pochodna funkcji?

Odpowiedzi: Wystawca i naturalny logarytm- funkcje są wyjątkowo proste pod względem pochodnych. Funkcje wykładnicze i logarytmiczne z dowolną inną podstawą będą miały inną pochodną, ​​którą przeanalizujemy później przejdźmy przez zasady różnicowanie.

Zasady różnicowania

Zasady czego? Ponownie nowy semestr, Ponownie?!...

Różnicowanie to proces znajdowania pochodnej.

To wszystko. Jak inaczej można nazwać ten proces jednym słowem? Nie pochodna. Matematycy nazywają różniczkę tym samym przyrostem funkcji. Termin ten pochodzi od łacińskiego słowa Differentia – różnica. Tutaj.

Wyprowadzając wszystkie te reguły, użyjemy na przykład dwóch funkcji i. Będziemy również potrzebować wzorów na ich przyrosty:

W sumie jest 5 zasad.

Stała jest usuwana ze znaku pochodnej.

Jeśli niektóre stała liczba(stała), następnie.

Oczywiście ta zasada działa również w przypadku różnicy: .

Udowodnijmy to. Niech tak będzie, albo prościej.

Przykłady.

Znajdź pochodne funkcji:

1. w pewnym momencie;
2. w pewnym momencie;
3. w pewnym momencie;
4. w tym punkcie.

Rozwiązania:

1. (pochodna jest taka sama we wszystkich punktach, ponieważ this funkcja liniowa, Pamiętać?);

Pochodna produktu

Tutaj wszystko jest podobne: wprowadźmy nową funkcję i znajdźmy jej inkrementację:

Pochodna:

Przykłady:

1. Znajdź pochodne funkcji i;
2. Znajdź pochodną funkcji w punkcie.

Rozwiązania:

Pochodna funkcji wykładniczej

Teraz twoja wiedza jest wystarczająca, aby dowiedzieć się, jak znaleźć pochodną dowolnej funkcji wykładniczej, a nie tylko wykładniki (zapomniałeś już, co to jest?).

Więc gdzie jest jakaś liczba.

Znamy już pochodną funkcji, więc spróbujmy sprowadzić naszą funkcję do nowej podstawy:

Do tego użyjemy prosta zasada: . Następnie:

Cóż, zadziałało. Teraz spróbuj znaleźć pochodną i nie zapominaj, że ta funkcja jest złożona.

Stało się?

Tutaj sprawdź sam:

Wzór okazał się bardzo podobny do pochodnej wykładnika: jak był, pozostaje taki sam, pojawił się tylko czynnik, który jest tylko liczbą, a nie zmienną.

Przykłady:
Znajdź pochodne funkcji:

Odpowiedzi:

To po prostu liczba, której bez kalkulatora nie da się obliczyć, czyli nie da się jej już zapisać w prostej formie. Dlatego zostawiamy to w tej formie w odpowiedzi.

Pochodna funkcji logarytmicznej

Tutaj jest podobnie: znasz już pochodną logarytmu naturalnego:

Dlatego, aby znaleźć dowolny logarytm o innej podstawie, na przykład:

Musimy sprowadzić ten logarytm do podstawy. Jak zmienić podstawę logarytmu? Mam nadzieję, że pamiętasz tę formułę:

Dopiero teraz zamiast tego napiszemy:

Mianownik jest po prostu stałą (liczbą stałą, bez zmiennej). Pochodną otrzymuje się bardzo prosto:

Pochodne funkcji wykładniczych i logarytmicznych prawie nigdy nie znajdują się w Unified State Examination, ale ich znajomość nie będzie zbyteczna.

Pochodna funkcji zespolonej.

Co się stało " złożona funkcja„? Nie, to nie jest logarytm ani arcustangens. Funkcje te mogą być trudne do zrozumienia (chociaż jeśli logarytm wydaje ci się trudny, przeczytaj temat „Logarity” i wszystko będzie dobrze), ale z matematycznego punktu widzenia słowo „złożony” nie oznacza „trudny”.

Wyobraź sobie mały przenośnik taśmowy: dwie osoby siedzą i wykonują pewne czynności z niektórymi przedmiotami. Przykładowo, pierwszy zawija tabliczkę czekolady w opakowanie, a drugi zawiązuje ją wstążką. W rezultacie powstał obiekt złożony: tabliczka czekolady owinięta i przewiązana wstążką. Aby zjeść tabliczkę czekolady, należy wykonać kroki w odwrotnej kolejności.

Stwórzmy podobny potok matematyczny: najpierw znajdziemy cosinus liczby, a następnie podniesiemy wynikową liczbę do kwadratu. Dostajemy więc liczbę (czekoladę), znajduję jej cosinus (opakowanie), a następnie podnoszę do kwadratu to, co otrzymam (przewiązuję wstążką). Co się stało? Funkcjonować. To jest przykład funkcji złożonej: gdy, aby znaleźć jej wartość, wykonujemy pierwszą akcję bezpośrednio ze zmienną, a następnie drugą akcję z tym, co wynika z pierwszej.

Możemy z łatwością wykonać te same kroki w odwrotnej kolejności: najpierw podnieś wynik do kwadratu, a następnie szukam cosinusa otrzymanej liczby: . Łatwo się domyślić, że wynik prawie zawsze będzie inny. Ważna funkcja funkcje złożone: gdy zmienia się kolejność działań, zmienia się funkcja.

Innymi słowy, funkcja złożona to funkcja, której argumentem jest inna funkcja: .

Dla pierwszego przykładu .

Drugi przykład: (to samo). .

Akcja, którą wykonamy jako ostatnia, zostanie wywołana funkcja „zewnętrzna”., oraz czynność wykonaną jako pierwsza – odpowiednio funkcję „wewnętrzną”.(są to nazwy nieformalne, używam ich jedynie w celu wyjaśnienia materiału prostym językiem).

Spróbuj sam określić, która funkcja jest zewnętrzna, a która wewnętrzna:

Odpowiedzi: Oddzielenie funkcji wewnętrznej i zewnętrznej jest bardzo podobne do zmiany zmiennych: na przykład w funkcji

1. Jaką czynność wykonamy jako pierwszą? Najpierw obliczmy sinus, a dopiero potem sześcian. Oznacza to, że jest to funkcja wewnętrzna, ale zewnętrzna.
   A oryginalną funkcją jest ich skład: .
2. Wewnętrzny: ; zewnętrzny: .
   Badanie: .
3. Wewnętrzny: ; zewnętrzny: .
   Badanie: .
4. Wewnętrzny: ; zewnętrzny: .
   Badanie: .
5. Wewnętrzny: ; zewnętrzny: .
   Badanie: .

Zmieniamy zmienne i otrzymujemy funkcję.

Cóż, teraz wyodrębnimy naszą tabliczkę czekolady i poszukamy pochodnej. Procedura jest zawsze odwrotna: najpierw szukamy pochodnej funkcji zewnętrznej, następnie mnożymy wynik przez pochodną funkcji wewnętrznej. W odniesieniu do pierwotnego przykładu wygląda to tak:

Inny przykład:

Sformułujmy więc w końcu oficjalną zasadę:

Algorytm znajdowania pochodnej funkcji zespolonej:

Wydaje się to proste, prawda?

Sprawdźmy na przykładach:

Rozwiązania:

1) Wewnętrzne: ;

Zewnętrzny: ;

2) Wewnętrzne: ;

(Tylko nie próbuj już tego ciąć! Spod cosinusa nic nie wychodzi, pamiętasz?)

3) Wewnętrzne: ;

Zewnętrzny: ;

Od razu widać, że jest to funkcja złożona na trzech poziomach: w końcu jest to już sama w sobie funkcja złożona i wydobywamy z niej również korzeń, czyli wykonujemy trzecią akcję (wkładamy czekoladę do w opakowaniu i ze wstążką w teczce). Ale nie ma powodu się bać: nadal „rozpakowujemy” tę funkcję w tej samej kolejności, co zwykle: od końca.

Oznacza to, że najpierw różnicujemy pierwiastek, potem cosinus, a dopiero potem wyrażenie w nawiasach. A potem to wszystko mnożymy.

W takich przypadkach wygodnie jest ponumerować działania. To znaczy wyobraźmy sobie to, co wiemy. W jakiej kolejności wykonamy działania, aby obliczyć wartość tego wyrażenia? Spójrzmy na przykład:

Im później akcja zostanie wykonana, tym bardziej „zewnętrzna” będzie odpowiednia funkcja. Sekwencja działań jest taka sama jak poprzednio:

Tutaj zagnieżdżenie jest zazwyczaj 4-poziomowe. Ustalmy kierunek działania.

1. Radykalne wyrażenie. .

2. Korzeń. .

3. Sinus. .

4. Kwadrat. .

5. Łączenie wszystkiego w jedną całość:

POCHODNA. KRÓTKO O NAJWAŻNIEJSZYCH RZECZACH

Pochodna funkcji- stosunek przyrostu funkcji do przyrostu argumentu dla nieskończenie małego przyrostu argumentu:

Podstawowe pochodne:

Zasady różnicowania:

Stała jest usuwana ze znaku pochodnej:

Pochodna sumy:

Pochodna produktu:

Pochodna ilorazu:

Pochodna funkcji złożonej:

Algorytm znajdowania pochodnej funkcji zespolonej:

1. Definiujemy funkcję „wewnętrzną” i znajdujemy jej pochodną.
2. Definiujemy funkcję „zewnętrzną” i znajdujemy jej pochodną.
3. Mnożymy wyniki pierwszego i drugiego punktu.

No cóż, temat się skończył. Jeśli czytasz te słowa, oznacza to, że jesteś bardzo fajny.

Bo tylko 5% ludzi jest w stanie samodzielnie coś opanować. A jeśli przeczytasz do końca, to jesteś w tych 5%!

Teraz najważniejsza rzecz.

Zrozumiełeś teorię na ten temat. I powtarzam, to... to jest po prostu super! Już jesteś lepszy od zdecydowanej większości Twoich rówieśników.

Problem w tym, że to może nie wystarczyć...

Po co?

Za pomyślne zdanie egzaminu Unified State Exam, za rozpoczęcie studiów z ograniczonym budżetem i, CO NAJWAŻNIEJSZE, za całe życie.

Nie będę Cię do niczego przekonywał, powiem tylko jedno...

Osoby, które otrzymały Dobra edukacja, zarabiają znacznie więcej niż ci, którzy ich nie otrzymali. To jest statystyka.

Ale to nie jest najważniejsze.

Najważniejsze, że są BARDZIEJ SZCZĘŚLIWI (są takie badania). Być może dlatego, że jest przed nimi dużo więcej otwarcia więcej możliwości i życie staje się jaśniejsze? nie wiem...

Ale pomyśl samodzielnie...

Czego potrzeba, aby na egzaminie Unified State Exam wypaść lepiej od innych i ostatecznie… być szczęśliwszym?

Zdobądź rękę, rozwiązując problemy z tego tematu.

Podczas egzaminu nie będziesz proszony o zadawanie teorii.

Będziesz potrzebować rozwiązywać problemy z czasem.

A jeśli ich nie rozwiązałeś (DUŻO!), na pewno popełnisz gdzieś głupi błąd lub po prostu nie będziesz miał czasu.

To jak w sporcie – trzeba to powtarzać wiele razy, żeby na pewno wygrać.

Znajdź kolekcję gdziekolwiek chcesz, koniecznie z rozwiązaniami, szczegółowa analiza i decyduj, decyduj, decyduj!

Możesz skorzystać z naszych zadań (opcjonalnie) i oczywiście je polecamy.

Aby lepiej radzić sobie z naszymi zadaniami, musisz pomóc przedłużyć żywotność podręcznika YouClever, który aktualnie czytasz.

Jak? Istnieją dwie opcje:

1. Odblokuj wszystkie ukryte zadania w tym artykule - 299 rubli.
2. Odblokuj dostęp do wszystkich ukrytych zadań we wszystkich 99 artykułach podręcznika - 499 rubli.

Tak, w naszym podręczniku mamy 99 takich artykułów i dostęp do wszystkich zadań oraz wszystkich ukrytych w nich tekstów można od razu otworzyć.

Dostęp do wszystkich ukrytych zadań jest zapewniony przez CAŁY okres istnienia witryny.

Podsumowując...

Jeśli nie podobają Ci się nasze zadania, znajdź inne. Tylko nie poprzestawaj na teorii.

„Rozumiem” i „Umiem rozwiązać” to zupełnie różne umiejętności. Potrzebujesz obu.

Znajdź problemy i rozwiąż je!