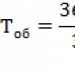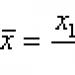Pytanie 16

Prawo rozkładu Weibulla jest jednym z najczęstszych w teorii niezawodności. Za tym prawem podąża trwałość zmęczeniowa produktów, czas do awarii produktów nienaprawialnych. Wykorzystując rozkład Weibulla można opisać różne przyczyny uszkodzeń: zmęczeniowe, nagłe, stopniowe. Prawo dystrybucji Weibulla uwzględnia awarie skrzyń biegów, ciągów, silników wiertniczych i ciągników.

Wskaźnik awaryjności produktu lub gęstość prawdopodobieństwa czasu sprawności produktu

Współczynnik awaryjności

MTBF

gdzie a, k są parametrami prawa rozkładu Weibulla;

Г(x) - funkcja gamma, której wartości podano w tabelach.

Dla k = 1 rozkład Weibulla staje się wykładniczy;

Gdy k = 2,5-3,5 - rozkład Weibulla jest bliski normalnemu.

Pytanie 17

Prawo rozkładu wykładniczego jest szczególnym przypadkiem prawa rozkładu Weibulla (k=1). Dotyczy produktów, które przeszły wstępne docieranie. Rozkład ten wykorzystywany jest również w analizie nagłych awarii pomp szlamowych i maszyn górniczych.

Prawdopodobieństwo bezawaryjnej pracy produktu w przedziale czasu od 0 do t

Prawdopodobieństwo uszkodzenia produktu w przedziale czasu od 0 do t

Funkcja różniczkowa lub gęstość prawdopodobieństwa rozkładu wykładniczego

Współczynnik awaryjności

Oczekiwanie matematyczne z rozkładem wykładniczym

Rozkład ten ma charakter empiryczny, uzyskany w wyniku badania szerokiej klasy rozkładów trwałości użytkowej. Doświadczenia w eksploatacji bardzo wielu urządzeń elektronicznych oraz znacznej ilości sprzętu elektromechanicznego wskazują, że charakteryzują się one trzema rodzajami zależności awaryjności od czasu, odpowiadającymi trzem okresom życia tych urządzeń.

Te trzy typy zależności awaryjności od czasu można uzyskać stosując do probabilistycznego opisu losowego czasu do uszkodzenia dwuparametrowy rozkład Weibulla, zgodnie z którym gęstość prawdopodobieństwa momentu uszkodzenia

gdzie  - parametr kształtu (określony przez selekcję w wyniku przetwarzania danych eksperymentalnych,  > 0);  - parametr skali,

Wskaźnik awaryjności jest określony przez wyrażenie

(3.1)

Prawdopodobieństwo dostępności

(3.2)

i średni czas do porażki

(3.3)

Zauważ, że dla parametru = 1 rozkład Weibulla staje się wykładniczy, a dla = 2 staje się rozkładem Rayleigha.

Przy 1 awaryjność maleje monotonicznie (okres docierania), a przy 1 monotonicznie wzrasta (okres zużycia), patrz rys. 3.1. Dlatego wybierając parametr  można uzyskać w każdym z trzech przekrojów taką teoretyczną krzywą (t), która dość ściśle pokrywa się z krzywą eksperymentalną, a następnie można obliczyć wymagane wskaźniki niezawodności wykonane w oparciu o znaną prawidłowość.

Rozkład Weibulla jest wystarczająco bliski dla wielu obiektów mechanicznych (np. łożysk kulkowych), można go wykorzystać do przyspieszonego testowania obiektów w trybie wymuszonym

3. Rozkład wykładniczy. Wykorzystywany jest częściej niż inne rozkłady, co jest typowe dla złożonych obiektów składających się z wielu elementów z rozkładami czasu działania. Przy stałej awaryjności daje proste wzory obliczeniowe. Jak zauważono, rozkład wykładniczy prawdopodobieństwa bezawaryjnej pracy jest szczególnym przypadkiem rozkładu Weibulla, gdy parametr kształtu  = 1. Rozkład ten jest jednoparametrowy, czyli jeden parametr  = const wystarczy do zapisania obliczone wyrażenie. Dla tego prawa prawdziwe jest również stwierdzenie odwrotne: jeśli awaryjność jest stała, to prawdopodobieństwo bezawaryjnej pracy w funkcji czasu jest zgodne z wykładniczym prawem:

Średni czas bezawaryjnej pracy zgodnie z wykładniczym prawem rozkładu przedziału bezawaryjnej pracy wyraża się wzorem:

(3.5)

Zastąpienie wartości  w wyrażeniu wartością 1 / T 1,

Dostawać . (3.6)

Znając zatem średni czas bezawaryjnej pracy T 1 (lub stały awaryjność ), w przypadku rozkładu wykładniczego można wyznaczyć prawdopodobieństwo bezawaryjnej pracy dla przedziału czasu od momentu powstania obiektu jest włączany w dowolnym momencie t.

4. Rozkład Rayleigha

Gęstość prawdopodobieństwa w prawie Rayleigha (patrz rys. 3.4) ma następującą postać



gdzie  jest parametrem rozkładu Rayleigha (równym modowi tego rozkładu ). Nie trzeba go mylić z odchyleniem standardowym:

.

Wskaźnik awaryjności wynosi:

(3.7)

Charakterystyczną cechą rozkładu Rayleigha jest prosta linia wykresu (t), zaczynając od początku.

Prawdopodobieństwo bezawaryjnej pracy obiektu w tym przypadku określa wyrażenie

(3.8)

MTBF

(3.9)

5. Obcięty rozkład normalny. Rozkład wyprowadzony z ograniczenia normalnego (gaussowskiego) na wartości dodatnie.

Prawo rozkładu normalnego charakteryzuje gęstość prawdopodobieństwa postaci

gdzie m x ,  x - odpowiednio oczekiwanie matematyczne i odchylenie standardowe zmiennej losowej x.

Analizując niezawodność instalacji elektrycznych w postaci zmiennej losowej, oprócz czasu często pojawiają się wartości prądu, napięcia elektrycznego i inne argumenty. Normalne prawo jest prawem dwuparametrowym, aby napisać, które musisz znać m x i  x.

Prawdopodobieństwo bezawaryjnej pracy określa wzór

(3.10)

a awaryjność - według wzoru

Na ryc. 3.5 przedstawia krzywe  (t), P (t) i  (t) dla przypadku  t  m t, charakterystyczne dla elementów stosowanych w układach automatyki.

4. Dystrybucja gamma. Rozkład Poissona i rozkład gamma są rozważane w związku, ponieważ oba charakteryzują te same procesy. Tylko w pierwszym przypadku awarie są traktowane jako zmienna, aw drugim czas. Dla rozkładu gamma
w- średni czas między awariami;

a- liczba awarii; G( a) to funkcja gamma równa
, Kiedy a-1 to liczba dodatnia.

Rozsądny wybór rodzaju praktycznego rozkładu czasu do awarii wymaga dużej liczby awarii wraz z wyjaśnieniem procesów fizycznych zachodzących w obiektach przed awarią.

W wysoce niezawodnych elementach instalacji elektrycznych, podczas eksploatacji lub testów niezawodności, zawodzi tylko niewielka część początkowo dostępnych obiektów. Dlatego wartość charakterystyk liczbowych znalezionych w wyniku przetwarzania danych eksperymentalnych silnie zależy od rodzaju oczekiwanego rozkładu czasu do uszkodzenia. Jak wynika z różnych praw czasu do awarii, wartości średniego czasu do awarii, obliczone na podstawie tych samych danych źródłowych, mogą różnić się setki razy. Dlatego należy zwrócić szczególną uwagę na kwestię wyboru modelu teoretycznego dla rozkładu czasu do awarii wraz z odpowiednim dowodem aproksymacji rozkładu teoretycznego i eksperymentalnego.

Ten rozkład jest najczęściej używany do badania wskaźników awarii w okresach wypalania i starzenia.

Niezawodność najczęstszych elementów sieci elektrycznych, takich jak transformatory mocy, linie kablowe, w dużej mierze zależy od niezawodności izolacji, której „wytrzymałość” zmienia się podczas pracy. Wytrzymałość izolacji, w zależności od warunków pracy i rodzaju wyrobu, determinowana jest wytrzymałością mechaniczną, elastycznością, co wyklucza możliwość powstawania odkształceń szczątkowych, pęknięć, rozwarstwień pod wpływem obciążeń mechanicznych, czyli niejednorodności.

Jednorodność i solidność struktury izolacji oraz jej wysoka przewodność cieplna wykluczają występowanie zwiększonego nagrzewania miejscowego, co nieuchronnie prowadzi do wzrostu stopnia niejednorodności wytrzymałości elektrycznej. Zniszczenie izolacji podczas pracy elementu następuje głównie w wyniku nagrzewania się prądami obciążenia oraz wpływu temperatury środowiska zewnętrznego. Obciążenia mechaniczne (drgania, odkształcenia, wstrząsy itp.) również prowadzą do zniszczenia izolacji.

Wśród wymienionych czynników, które określają żywotność izolacji tych elementów sieci elektrycznych, jednym z głównych czynników jest starzenie termiczne. Na podstawie badań eksperymentalnych uzyskano znaną regułę „ośmiu stopni”, zgodnie z którą wzrost temperatury izolacji wykonanej na bazie organicznej średnio o każde osiem stopni skraca żywotność izolacji o połowę. Obecnie w zależności od klasy zastosowanej izolacji stosuje się reguły sześcio-, ośmio-, dziesięcio- i dwunastostopniowe.

Żywotność izolacji w zależności od temperatury ogrzewania:

T i = ALE e-γς, (5.43)

gdzie ALE -żywotność izolacji przy ς = 0 - pewna wartość warunkowa;

γ- współczynnik charakteryzujący stopień starzenia izolacji w zależności od klasy;

ς - temperatura przegrzania izolacji.

Innym ważnym czynnikiem powodującym intensywne starzenie się izolacji są procesy elektryczne podczas nagłych zmian prądu, na przykład przy gwałtownie zmieniającym się obciążeniu transformatora mocy, przepięciach i zrzucaniu obciążenia, poprzez prądy zwarciowe. Właściwości mechaniczne wytrzymałości izolacji zależą również od temperatury. Wytrzymałość mechaniczna izolacji gwałtownie spada w miarę jej nagrzewania, ale jednocześnie staje się ona bardziej elastyczna.

Pod wpływem zmiennych niekorzystnych warunków zwiększa się niejednorodność materiału, np. mikropęknięcia wnikają w głąb izolacji i w przypadku przypadkowego zwiększenia napięcia mogą spowodować przebicie izolacji. Przyczyną niepowodzenia może być nawet niewielka niejednorodność materiału.

Liczba niekorzystnych efektów (termicznych lub elektromechanicznych) powodujących przebicie izolacji jest funkcją, która maleje w zależności od wielkości niejednorodności. Ta liczba jest minimalna dla największych niejednorodności (pęknięcia, rozwarstwienia itp.). Tak więc liczba niekorzystnych skutków, czyli żywotność izolacji, musi być zgodna z prawem rozkładu minimalnej liczby niezależnych TS – liczbami niekorzystnych skutków odpowiadających niejednorodnościom o różnych rozmiarach, tj. jeśli Ti jest czasem bezawaryjnej pracy całej izolacji, a Tii to czas sprawności i-tego odcinka (i = 1, 2,..., n), to:

T i = min ( T u1, T oraz 2,…, T w). (5.44)

Zatem, aby wyznaczyć prawo rozkładu czasu sprawności dla takiego obiektu, jakim jest izolacja elementu sieci elektrycznej, konieczne jest wyznaczenie prawdopodobieństwa rozkładu minimalnego czasu sprawności dla sumy wszystkich odcinków. Co więcej, najciekawszy jest przypadek, w którym prawa rozdziału czasu sprawności poszczególnych odcinków mają charakter arbitralny, ale forma praw rozdziału jest taka sama, tzn. nie ma odcinków drastycznie różniących się.

Pod względem niezawodności sekcje takiego systemu odpowiadają połączeniu szeregowemu. Dlatego funkcją dystrybucji czasu pracy takiego systemu jest:

q c(t) = 1 – n. (5.45)

Ponadto, za pomocą przekształceń matematycznych, wyprowadzany jest wzór, w którym głównym parametrem jest „próg czułości”, tj. element ma gwarancję, że nie zawiedzie w przedziale czasu (0, t0) (w szczególnym przypadku t0 = 0). Jeśli rozkład nie ma progu czułości t0 , wtedy nazywa się prawo dystrybucji Dystrybucja Weibulla:

gdzie c > 0 jest jakimś stałym współczynnikiem;

α jest parametrem rozkładu.

To prawo rozkładu jest dość często stosowane w przybliżaniu rozkładu czasu sprawności dla systemów o skończonej liczbie szeregowo (pod względem niezawodności) połączonych elementów (długie linie ze znaczną liczbą sprzężeń itp.).

Gęstość dystrybucji:

(5.47)

Na α = 1, gęstość rozkładu zamienia się w zwykłą funkcję wykładniczą (patrz rysunek 5.12).

Rysunek 5.12 - Funkcja rozkładu różnicowego czasu sprawności izolacji zgodnie z prawem

Weibulla

Rysunek 5.13 - Wskaźnik awaryjności przy

Dystrybucja Weibulla

Wskaźnik awaryjności rozkładu gęstości zgodnie z prawem Weibulla (patrz rysunek 5.13):

λ(t) = αctα-1. (5.48)

Wskaźnik awaryjności dla tego prawa, w zależności od parametru rozkładu, może rosnąć, pozostawać na stałym poziomie (prawo wykładnicze) i maleć.

Jak widać na rysunkach 5.12 i 5.13, prawo rozkładu wykładniczego jest szczególnym przypadkiem prawa Weibulla dla α = 1 (λ = const). Na α = 2, funkcja rozkładu czasu sprawności zbiega się z prawem Rayleigha, gdzie α »1 jest dość dobrze przybliżone przez prawo rozkładu normalnego w okolicach średniego czasu bezawaryjnej pracy.

Przy odpowiednim doborze parametru α Wykorzystując prawo Weibulla można opisać niezawodność zarówno elementów starzeniowych (okres starzenia i zużycia), w których wzrasta λ(t), jak i elementów z wadami ukrytymi (okres docierania), w których λ( t) maleje z upływem czasu.

Matematyczne oczekiwanie (czas średni) czasu sprawności i wariancji rozkładu według prawa Weibulla:

T i.sr = Г(1+1/α) c-1/α, (5,49)

D(Ti) = c-2/α [Г(1+2/α) – Г2(1+1/α)]. (5.50)

gdzie G( X) to funkcja gamma.

Jeśli znane jest prawo rozkładu czasu wystąpienia awarii produktu (na przykład wybrane na podstawie danych eksperymentalnych), możliwe jest obliczenie wskaźników niezawodności produktów. Często występują rozkłady Weibulla, wykładniczego, Rayleigha i inne.

Rozkład Weibulla ma dwa parametry: δ jest parametrem kształtu (nie mylić z odchyleniem standardowym) i λ jest parametrem skali (nie mylić ze wskaźnikiem awaryjności).

W przypadku rozkładu Weibulla wskaźnik niepowodzeń wynosi

λ(t)= λδt δ-1

Trzy przekroje charakterystyczne dla lambli na ryc. 15.1 odpowiada rozkładom Weibulla o różnych parametrach λ oraz δ . Tak więc w okresie docierania δ <1, в рабочей области δ =1 (w tym przypadku rozkład Weibulla odpowiada rozkładowi wykładniczemu), w obszarze zużycia δ >1 (kiedy δ =2 rozkład Weibulla odpowiada rozkładowi Rayleigha).

Przykład 16.1. Na podstawie danych eksperymentalnych stwierdzono, że charakterystyka lambda wyrobów wytwarzanych przez przedsiębiorstwo jest zbliżona do pokazanej na ryc. 15.1, a odcinki krzywej odpowiadają rozkładowi Weibulla o parametrach wskazanych w tabeli. 16.1.

Fragment obliczenia dla przykładu 16.1 pokazano na ryc. 16.1.

Rys.14.1. Fragment obliczenia na przykład 16.1.

Wprowadź wartości parametrów skali i odpowiadające im wartości parametrów kształtu, a także kolumnę wartości czasu. Następnie obliczamy kolumny awaryjności w obszarze od 50 do 5000 godzin w odstępie 50 godzin dla każdej z trzech par parametrów skali i kształtu. Budujemy wykresy wszystkich trzech krzywych (ryc. 16.2).

Rys.16.2. Działki dystrybucyjne Weibulla.

Obszar docierania na charakterystyce lambda będzie powyżej punktu 1, obszar roboczy - między punktami 1 i 2, obszar zużycia - powyżej punktu 2.

Jak widać z obliczonych danych, obszar roboczy zaczyna się po około 200 godzinach, kiedy wskaźnik awaryjności w nim staje się większy niż wskaźnik awaryjności w obszarze docierania. Obszar roboczy kończy się po około 4000 h, kiedy awaryjność w nim spada poniżej awaryjności w obszarze zużycia. Tak więc, aby uporządkować żądane wartości wskaźnika awaryjności w kolumnie λ(t) kopiuj za pomocą polecenia Kopiuj - Wklej specjalnie - Wartości pasujące zakresy z kolumn Bieganie w, Niewolnik. region. oraz Nosić. Na podstawie tych wartości budujemy charakterystykę lambda.

Rys.16.3. Charakterystyka lambdy.

Ćwiczenie.

1. Uruchom przykład 16.1.

Laboratorium #17

Rozkłady Rayleigha i rozkład wykładniczy

Przy obliczaniu wskaźników niezawodności

Rozkład wykładniczy jest szczególnym przypadkiem rozkładu Weibulla, gdy δ =1. Rozkład wykładniczy ma jeden parametr λ . Przy wykładniczym rozkładzie czasów awarii produktów wskaźnik awaryjności

λ(t)= λ=const

Р(t)=e -λ t

MTBF

Т=1/λ

Rozkład Rayleigha jest szczególnym przypadkiem rozkładu Weibulla, gdy δ =2. Rozkład Rayleigha ma jeden parametr δ * . Jednocześnie wskaźnik awaryjności

λ(t)=t/ δ * 2

Prawdopodobieństwo dostępności

MTBF

Ćwiczenie.

1. Wyrób wytwarzany przez przedsiębiorstwo ma rozkład wykładniczy czasu wystąpienia awarii ze współczynnikiem awaryjności 3∙10 -5 1/h. Oblicz prawdopodobieństwo bezawaryjnej pracy w terenie od 0 do 20 000 godzin w odstępach co 500 godzin i wykreśl P(t)

2. Wyrób wytwarzany przez przedsiębiorstwo posiada rozkład Rayleigha czasu wystąpienia awarii z parametrem rozkładu δ * = 1000 godzin Oblicz prawdopodobieństwo bezawaryjnej pracy w terenie od 10 do 1000 godzin w odstępach co 10 godzin i buduj wykresy P(t) oraz λ(t). Oblicz średni czas do awarii.

Laboratorium #18

Planowanie testu pojedynczej próbki

Planując testy kontrolne pod kątem wiarygodności przy użyciu metody pojedynczej próby, ustalany jest jednoetapowy plan kontroli, który obejmuje czas testu t i, wielkość próbki n i numer akceptacji C. Numer akceptacji to maksymalna możliwa liczba produktów, które nie przeszły testu, przy której partia produktów została uznana za odpowiednią.

Podczas planowania brane są pod uwagę interesy dostawcy i klienta – planowanie poziomu akceptacji i odrzucenia, lub interesy samego klienta – planowanie poziomu odrzucenia.

Planując poziomy akceptacji i odrzucenia, określa się:

1. Dopuszczalna wartość prawdopodobieństwa bezawaryjnej pracy produktu losowo wybranego z partii Rocznie.

2. Odpowiadające ryzyko dostawcy α to prawdopodobieństwo, że duża część zostanie odrzucona.

3. Minimalna wartość prawdopodobieństwa bezawaryjnej pracy Pβ, tj. odrzucenie (gwarantowana) wartość prawdopodobieństwa bezawaryjnej pracy (zawsze) Rocznie. >Pβ).

4. Odpowiadające ryzyko klienta β - prawdopodobieństwo, że wadliwa partia zostanie uznana za odpowiednią.

Planując według poziomu odrzucenia, ustaw Pβ oraz β . Planowanie poziomu odrzucenia jest stosowane wewnętrznie przez dostawców w celu zapewnienia, że ​​niezawodność spełnia wymagania klientów.

W metodzie pojedynczego pobierania próbek jedna próbka jest pobierana z partii. Jeśli zawiera liczbę nieudanych produktów d ≤ C partia zostaje przyjęta, w przeciwnym razie zostaje odrzucona. Jednocześnie, jeśli prawo rozkładu wskaźnika niezawodności nie jest znane, czas testu t i weź równe gwarantowanemu czasowi tr, na którym ustawione jest minimalne prawdopodobieństwo bezawaryjnej pracy Pβ.

Wartości n oraz C znaleźć w następujący sposób.

Prawdopodobieństwo P(Q) przyjąć partię w zależności od proporcji wadliwych produktów w partii, Q przy określonych wartościach C, N(wielkość partii) i n opisany przez rozkład hipergeometryczny. Na n ≤ 0,1 N, co zwykle ma miejsce w praktyce, zamiast rozkładu hipergeometrycznego z dobrym przybliżeniem można zastosować rozkład dwumianowy, który jest łatwiejszy do obliczenia w Excelu.

Planując według poziomu odrzuceń dla danego Pβ wybierz takie wartości n oraz C, do P(Q), obliczony z rozkładu dwumianowego, był równy (najbliższy) ryzyku dostawcy β :

P(Q) = β (18.1)

Dla określonych warunków istnieje wiele par n oraz C, wystarczająco dobrze spełniające równanie (18.1). Ale Z jest wybierany jako mały, ponieważ wraz ze wzrostem, wielkość próbki gwałtownie wzrasta n. Jednak zwykle nie C = 0, ponieważ jest to wartość najbardziej niekorzystna dla producenta.

Planując poziomy akceptacji i odrzucenia, użyj równania (18.1) i równania

P(Q) = 1-α (18.2)

Ulec poprawie n oraz C tak, aby (18.1) i (18.2) trzymały się jednocześnie. Jednocześnie dla określonych warunków istnieje para minimalnych możliwych wartości n oraz C, które najlepiej spełniają (18.1) i (18.2).

Przykład 18.1. W przedsiębiorstwie konieczne jest przetestowanie partii wyprodukowanych wyrobów, aby upewnić się, że niezawodność wyrobów spełnia wymagania klienta, którymi są: minimalne prawdopodobieństwo bezawaryjnej pracy wynosi 0,92 na 300 godzin z ryzykiem dostawcy 0,1. Znajdź plan kontroli niezawodności.

Możliwa implementacja przykładu 18.1 jest pokazana na ryc. 18.1.

Wprowadzamy dane początkowe Pβ oraz β , numer akceptacji - np. 2 (później w razie potrzeby można tę wartość zmienić), a także kolumna możliwych wartości objętości testowej n(Wskazane jest co najmniej do 1000).

Rys.18.1. Opcja kalkulacji na przykład 18.1.

Teraz musimy znaleźć jedną z wartości n, pod którym warunek (18.1) jest spełniony. W tym celu obliczamy wartości prawdopodobieństwa przyjęcia partii P(Q) w zależności od ilości testów, używając funkcji ROZKŁAD.DWUM. Okno dialogowe, które otwiera się po wybraniu funkcji ROZKŁAD.DWUM zawiera cztery wiersze do wprowadzania danych:

Liczba_sukcesów. Sądząc po podpowiedzi do tego wiersza, musisz wprowadzić liczbę udanych prób. Liczba udanych prób w tym przypadku jest rozumiana jako liczba elementów próbki, które mają określony atrybut. W naszym przypadku jest to maksymalna możliwa liczba wadliwych elementów w próbce, przy której partia jest akceptowana, tj. należy odnieść się do komórki z wartością numeru akceptacji.

Liczba prób. Należy odnieść się do kuwety z wartością objętości testowej (wielkość próbki).

Prawdopodobieństwo_sukcesu. W naszym przypadku jest to prawdopodobieństwo, że produkt losowo wybrany z partii będzie wadliwy, tj. prawdopodobieństwo awarii równe 1-Pβ .

Całka. Ponieważ partia jest akceptowana dla dowolnej liczby wadliwych elementów w próbce od 0 do C, funkcja rozkładu dwumianowego musi być integralna, a zatem wartość PRAWDA.

W przypadkach, w których n< C , obliczenia za pomocą funkcji ROZKŁAD.DWUM dadzą błąd (okazuje się, że wartość #LICZBA!). Jednocześnie oczywiste jest, że w tych wierszach P(Q)=1.

Pożądana wartość n będzie w wierszu arkusza kalkulacyjnego, gdzie P(Q) = β, a dokładniej, gdzie jest wartość bezwzględna P(Q)-β minimalna, więc obliczamy odpowiednie wartości. Ale ponieważ w n< C obliczenia P(Q) podać błąd, użyj funkcji JEŻELI. Kiedy warunek logiczny jest prawdziwy n< С ustaw wartość 1-β. Jeśli warunek logiczny jest fałszywy, znajdujemy moduł (funkcja ABS) P(Q) - β.

Uzyskiwanie kolumny wartości |P(Q)-β|, możesz już wizualnie znaleźć w nim minimalną wartość i odpowiednią ilość testów. Aby jednak zautomatyzować obliczenia, należy znaleźć żądany numer wiersza za pomocą formuły tablicowej, tak jak w pracy laboratoryjnej nr 2. Przypomnienie: aby wprowadzić formułę jako formułę tablicową, naciśnij kombinację klawiszy CTRL + SHIFT + ENTER (formuła CSE ), po czym formuła zostanie zawarta w nawiasach klamrowych. W takim przypadku wpisywanie nawiasów klamrowych z klawiatury nie da pożądanego rezultatu. Ponadto za każdym razem, gdy przesuwasz kursor do wiersza formuły tablicowej, musisz ponownie nacisnąć klawisze CTRL + SHIFT + ENTER, w przeciwnym razie formuła nie będzie już postrzegana jako formuła tablicowa.

Na podstawie numeru linii obliczamy ilość testów. Tak więc, zgodnie z rysunkiem 18.1, odejmujemy 3 od znalezionego numeru wiersza, ponieważ wartości w kolumnach zaczynają się dopiero od czwartego wiersza.

Przy liczbie akceptacji 2 otrzymujemy wymaganą ilość testów 65. Tak więc plan kontroli niezawodności: n = 65, C = 2, ti = 300 godz.

Ale możesz ustawić dowolny inny numer akceptacji i uzyskać odpowiednią liczbę testów.

Przykład 18.2. Znajdź plan kontroli niezawodności partii produktów według poziomów akceptacji i odrzucenia, jeśli został podany: Рα= 0,96, α = 0,1, P β= 0,92, β = 0,1 dla 300 godzin testowania.

Możliwa implementacja przykładu 18.2 jest pokazana na ryc. 18.2.

Rys.18.2. Opcja kalkulacji na przykład 18.2.

Wprowadzamy dane początkowe Rocznie, α, Pβ oraz β , dowolny numer akceptacji - np. 2 (wtedy ta wartość), a także kolumna możliwych wartości​​objętości testowej n(Wskazane jest co najmniej do 4000). Obliczamy kolumny wartości P(Q) α , |P(Q) α -1+α|, P(Q) β, |P(Q) β -β|. Wartości P(Q) α i P(Q) β są obliczane za pomocą funkcji ROZKŁAD.DWUM, natomiast w oknie dialogowym funkcji w wierszu Prawdopodobieństwo_sukcesu wpisz 1 - Pa lub 1-Pβ, w zależności od kolumny. Dalej, korzystając z formuł tablicowych, zgodnie z (16.1) i (16.2), znajdujemy numery wierszy, w których odpowiednio wartości bezwzględne P(Q) α-1+α oraz P(Q) β-β minimalna (najbliższa zeru). Na podstawie tych numerów wierszy znajdujemy objętości próbek nα oraz n β zapewniając podane α oraz β , a także moduł różnicy między nimi. Następnie dobieramy taką wartość liczby akceptacji (minimalną możliwą), aby ten moduł różnicy był minimalny (najczęściej od 0 do 4). Plan kontroli niezawodności (plan testów) będzie zawierał wybraną wartość numeru akceptacji oraz jedną ze znalezionych wartości nα oraz n β lub jedna z wartości pośrednich między nimi. Może być traktowany jako zakres testowy nśrednia między nα oraz nβ. Jednocześnie realne ryzyko dostawcy i konsumenta będzie się nieco różnić od podanych.

W naszym przykładzie otrzymujemy plan kontroli niezawodności: n = 218, C = 12, t i= 300 godz.

Ćwiczenie.

1. Wykonać obliczenia zgodnie z przykładem 18.1 dla różnych wartości​​liczby akceptacji, minimalnego prawdopodobieństwa bezawaryjnej pracy oraz ryzyka odbiorcy wskazanego w tabeli. 18.1. Zapisz wyniki w tabeli 18.1 na osobnej kartce książki elektronicznej. Wyciągnij wnioski na temat tego, jak wzrost liczby odbiorów, minimalne prawdopodobieństwo bezawaryjnej pracy oraz ryzyko konsumenta wpływają na ilość testów.

Tabela 18.1.

numer akceptacji	Pβ	Zakres badań
β = 0,05	β = 0,1	β = 0,2
	0,92
0,94
	0,92
0,94
	0,92
0,94
	0,92
0,94

2. Wykonać obliczenia zgodnie z przykładem 18.2 z różnymi wartościami akceptowalnego prawdopodobieństwa bezawaryjnej pracy, minimalnego prawdopodobieństwa bezawaryjnej pracy, ryzyka producenta i konsumenta, wskazanych w tabeli . 18.2. Zapisz wyniki w tabeli 18.2 na osobnej kartce książki elektronicznej. Wyciągnięcie wniosków na temat tego, jak wzrost akceptowalnego prawdopodobieństwa bezawaryjnej pracy, minimalne prawdopodobieństwo bezawaryjnej pracy, ryzyko producenta i ryzyko konsumenta wpływają na ilość badań i liczbę odbiorów

Tabela 18.2.

Pa	Pβ	α=β=0,05	α=β=0,1	α=β=0,2
n	C	n	C	n	C
0,94	0,90
0,91
0,95	0,90
0,91

Laboratorium #19

Sekwencyjny plan testów

W planie sekwencyjnym liczba pozycji do przetestowania lub czas testowania nie są z góry określone, ale zależą od wyniku obserwacji. Testom poddawany jest produkt lub kilka produktów (zgodnie z programem badań). Następnie na podstawie uzyskanych wyników podejmowana jest jedna z trzech decyzji: zaakceptować partię, odrzucić partię lub kontynuować badanie. Jeśli testy są kontynuowane, liczba obserwacji jest kolejno sumowana n i ilość awarii r. Na podstawie wyników sumowania obserwacji i awarii budowany jest wykres (rys. 19.1)

Rys.19.1. Harmonogram planu testów sekwencyjnych

Na rysunku 19.1 wiersze 1 i 2 to granice odrzucenia, 3 i 4 to granice akceptacji, 5 to linia wdrażania procesu niepowodzenia, n- łączną liczbę obserwacji (testowanych produktów) w momencie testowania, r- łączna liczba awarii w momencie testowania, c- ograniczenie (odrzucenie) całkowitej liczby awarii, N- maksymalna możliwa (dopuszczalna) liczba uwag przed podjęciem decyzji o przyjęciu lub odrzuceniu. Wartości z oraz N można znaleźć przez jednokrotne pobranie próbki (patrz przykład 18.2, gdzie są odpowiednio oznakowane) Z oraz n).

Na przykład, zgodnie z tym harmonogramem, na pierwszym etapie przetestowano n 1 produktów i było r 1 uszkodzeń, na pierwszym i drugim etapie przetestowano łącznie n 2 produkty i było r 2 uszkodzeń itd. Jeżeli na którymś etapie testowania linia 5 przekroczy linię 1 lub 2, partia jest odrzucana. Jeśli linia 5 przecina linie 3 lub 4, partia jest uważana za dobrą.

Linia niedopasowania (odrzucenia) 1 jest obliczana za pomocą równania r = an+r0.

Linia zgodności (akceptacji) 4 jest obliczana za pomocą równania r = a(n-n 0).

Tutaj D = (1 - Pβ)(1-Pα)

Używając tylko wierszy 1 i 4 jako wierszy akceptacji i odrzucenia, uzyskuje się nieskrócony plan sekwencyjny, gdy używane są również wiersze 2 i 3, uzyskuje się obcięty plan sekwencyjny.

Plan sekwencyjny można również wdrożyć analitycznie, tj. bez kreślenia. Jednocześnie na pewnym etapie badań partia jest uważana za wadliwą, jeżeli spełniony jest jeden z poniższych warunków:

r > an+r0 (19.1)

r > c (19.2)

Partia jest uważana za akceptowalną, jeśli spełniony jest jeden z następujących warunków:

r< a(n-n 0) (19.3)

n > N (19.4)

Jeśli żaden z tych warunków nie jest spełniony, test jest kontynuowany.

Zaletą planu sekwencyjnego w porównaniu z jednostopniowym (pojedynczą próbą) jest minimalizacja średniej liczby obserwacji. Oszczędności na elementach testowych mogą wynieść nawet 40% lub więcej w porównaniu z planem jednoetapowym. Jednak plan sekwencjonowania nie jest odporny na możliwe dotarcie produktów na początku testowania, co skutkuje zwiększonym ryzykiem dostawcy.

Przykład 19.1. Partia produktów jest testowana zgodnie z planem sekwencyjnym. Na każdym etapie przeprowadzany jest test n ja= 5 produktów. Zapytał Рα= 0,95, α = 0,1, P β= 0,9, β = 0,1. Liczba nieudanych produktów sekwencyjnie według etapów r ja było: 1 0 2 0 0 0 1 0 0 0 0 2 0 0 0 0 1 1 0 0 2 1 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 1. Na jakim etapie powinny być badania zakończone iz jakim skutkiem? Znajdź rozwiązanie analitycznie i graficznie.

Fragment wykonania przykładu 19.2 pokazano na ryc. 19.2.

Rys.19.2. Opcja kalkulacji na przykład 19.2.

Wprowadzamy dane początkowe, obliczamy D, a, r0, n0. Następnie w arkuszu kalkulacyjnym utworzonym w przykładzie 18-2 obliczamy z oraz N(w przykładzie 18.2 Z oraz n) i wprowadź ich wartości do arkusza kalkulacyjnego. (należy zauważyć, że w GOST R 27.403-2009 „Plany badań monitorowania prawdopodobieństwa bezawaryjnej pracy” podano wyższe wartości z oraz N). Wpisz w kolumnie wartości numerów etapów testowych i (z uwzględnieniem możliwości przeliczenia wg innych danych do ok. 1000). Kolejną sumę prób znajdujemy według wzoru n = i∙n i. Wprowadzanie wartości r ja. Następnie oblicz kolumnę r. Aby to zrobić, w pierwszej komórce G4 tworzymy link do komórki F4. W drugiej komórce kolumny (która odpowiada drugiemu etapowi testowania) podsumowujemy wartość w poprzedniej komórce G4 oraz liczbę awarii na tym etapie. Skopiuj wynikową formułę z tej komórki do pozostałych komórek w kolumnie r.

Następnie wypełnij kolumny MAŁŻEŃSTWO? oraz DOBRY?. W kolumnie MAŁŻEŃSTWO? użyj funkcji JEŻELI. W oknie dialogowym tej funkcji wpisujemy wyrażenie logiczne (19.1) i zamykając je w nawiasach dodajemy funkcję OR. W otwartym oknie dialogowym tej funkcji wprowadź wyrażenie logiczne (19.2). Następnie ustaw kursor na pasku formuły na słowo JEŻELI. W oknie dialogowym funkcji JEŻELI, które się otworzy, jeżeli wyrażenia logiczne (19.1) lub (19.2) są prawdziwe, wyświetlamy komunikat „Odrzucenie” (tzn. paczka jest odrzucana). Jeśli te wyrażenia są fałszywe, wyświetlamy komunikat „Dalej” (tzn. testy powinny być kontynuowane). W kolumnie DOBRY? użyj również funkcji JEŻELI, podobnie jak to się robi dla kolumny MAŁŻEŃSTWO?, używając wyrażeń logicznych (10.3) i (19.4). Jeśli (19.3) lub (19.4) jest prawdziwe, wyświetlamy komunikat „Dobra” (tzn. partia jest uznana za dobrą). Jeśli te wyrażenia są fałszywe, wyświetlamy komunikat „Dalej” (tzn. testy powinny być kontynuowane).

Jeśli wiersz o niższym numerze w arkuszu kalkulacyjnym brzmi „Odrzucono”, partia jest odrzucana. Jeśli komunikat „Dobra” pojawi się w wierszu arkusza kalkulacyjnego o niższym numerze, partia zostanie uznana za dobrą.

W przypadku rozwiązania graficznego wprowadzamy kolumny do arkusza kalkulacyjnego Linia 1 oraz Linia 4. W górnych komórkach kolumn Linia 1 oraz Linia 4 obliczamy odpowiednie wartości i opiniujemy powstałe formuły na końcu kolumn (nie zapomnij odpisać adresowania bezwzględnego). Następnie budujemy diagram Wykres punktowy z wartościami połączonymi słupkami. Uwzględnij wartości kolumn na wykresie n, r, Linia 1 oraz Linia 4. Maksymalne wartości skali n oraz r korzystając z menu kontekstowego, ograniczamy wartości odpowiednio do N i c, co ograniczy zasięg wykresu do linii 2 i 3.

Wynikowy wykres pokazano na ryc. 19.3.

Rys.19.3. Graficzne rozwiązanie przykładu dla przykładu 19.2.

Jak widać na wykresie, linia 5 przecina linię 1, więc partię należy uznać za wadliwą. Najeżdżając kursorem myszy na punkt przecięcia linii 1 z linią 5, możesz użyć podpowiedzi do określenia, w którym n testy powinny zostać zakończone.

Ćwiczenie.

1. Wykonaj obliczenia zgodnie z przykładem 19.1.

2. Partia produktów jest testowana zgodnie z planem sekwencyjnym. Zapytał Рα= 0,97, α = 0,1, P β= 0,92, β = 0,1. Liczba produktów testowanych na każdym etapie n ja i liczbę nieudanych produktów sekwencyjnie według etapów r ja pokazano w tabeli 19.1. Określ analitycznie, na jakim etapie testy powinny zostać zakończone i z jakim wynikiem? Wpisz wyniki w tabeli. 19.1.

Tabela 19.1.

Opcja	n ja	r ja	Finałowy etap	Impreza (dobre / małżeństwo)
		1 0 1 0 0 0 1 0 0 0 0 2 0 0 0 0 1
		2 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1
		1 1 1 2 0 1 0 2 0 1 0 2
		0 1 0 1 0 1 0 0 0 1 0 1 0 0 0 0 1
		1 1 0 1 0 2 0 0 1 1
		1 0 2 0 1 0 2 0 0 1 2 1 0 1 0
		0 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0
		2 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 1
		1 0 1 0 1 0 0 0 1 0 0 0 0 0 1 0 2
		0 0 1 0 2 1 0 0 0 0 1 2

BIBLIOGRAFIA

Kobzar AI Stosowana statystyka matematyczna. Dla pracowników inżynieryjno-naukowych - M .: FIZMATLIT, 2006. - 816 s.

Stiepnow M.N. Statystyczne metody przetwarzania wyników badań mechanicznych: Podręcznik. – M.: Mashinostroenie, 1985. – 232 s.

Zapewnienie metrologiczne badań wyrobów do celów oceny zgodności: Poradnik metodologiczny. - M: VNIIMS, 2003.

Smirnov N.V., Dunin-Barkovsky I.V. Kurs teorii prawdopodobieństwa i statystyki matematycznej do zastosowań technicznych. - M.: Nauka, 1969. - 512 s.

Tyurin Yu.N. Nieparametryczne metody statystyki. - M.: Wiedza, 1978. - 64 s.

Taylor J. Wprowadzenie do teorii błędu. Za. z angielskiego. – M.: Mir, 1985. – 272 s.

Khan G., Shapiro S. Modele statystyczne w problemach inżynierskich: Per. z angielskiego. - M.: Mir, 1969. - 400 s.

Gludkin OP Metody i urządzenia do badania OZE i EVS. - M.: Wyższe. szkoła., 2001. - 335 s.

Mlitsky V.D., Beglaria V.Kh., Dubitsky L.G. Badania urządzeń i przyrządów pomiarowych pod kątem wpływu czynników zewnętrznych. M.: Mashinostroenie, 2003. - 567 s.

Testowanie radioelektronicznego, elektronicznego sprzętu komputerowego i testowego / wyd. A.I. Korobova M.: Radio i komunikacja, 2002. - 272 s.

Siergiej A.G. Metrologia: Podręcznik. – M.: Logos, 2005. – 272 s.

Fedorov V., Sergeev N., Kondrashin A. Kontrola i testowanie w projektowaniu i produkcji sprzętu radioelektronicznego - Technosphere, 2005. - 504p.

Ostreikovsky V.A. Teoria niezawodności: podręcznik dla szkół średnich. - M.: Wyższe. szkoła , 2003r. - 463 s.

Niezawodność systemów technicznych: podręcznik. Yu K. Belyaev, V. A. Bogatyrev, V. V. Bolotin i inni; Wyd. I. A. Uszakowa. - M.: Radio i komunikacja, 1985.-608 s.

Kotelenets N.F., Kuzniecow N.L. Badania i niezawodność maszyn elektrycznych: Podręcznik. - M.: Wyższe. szkoła, 1988. - 232 s.

Zalyazhnykh V.V., Koptelov A.E. Statystyczne metody kontroli i zarządzania jakością: Podręcznik. - Archangielsk: Wydawnictwo Archangielskiego Państwowego Uniwersytetu Technicznego, 2004. - 88 s.

GOST R 27.403-2009 Niezawodność w inżynierii. Plany testowe do kontroli prawdopodobieństwa bezawaryjnej pracy.

Dolzhenkov V.A., Kolesnikov Yu.V. Microsoft Excel 2002 w oryginale. Petersburg: BHV-Petersburg, 2002. - 1072 s.

WSTĘP…………………………………………………………...……….3

PODSTAWOWE SYMBOLE………………………………………………4

OCENA WYNIKÓW BADAŃ……………………………….5

Praca laboratoryjna nr 1. Estymatory punktowe i przedziałowe……..5

Praca laboratoryjna nr 2. Ustalenie zakresu badań………10

Laboratorium #3: Sprawdzanie akceptowalności wyników

testy………………………………………………………………..17

WYKLUCZENIE WIELKICH BŁĘDÓW………………………………………25

Praca laboratoryjna nr 4. Kryterium N.V. Smirnowa………………25

Praca laboratoryjna nr 5. Kryterium Dixona……………………...32

Praca laboratoryjna nr 6. Kryterium Irwina……………………….37

Praca laboratoryjna nr 7. Kryterium Chauveneta………………………39

Praca laboratoryjna nr 8. Kryterium Romanowskiego………………..41

OCENA RODZAJU DYSTRYBUCJI

WARTOŚĆ LOSOWA……………………………………………43

Praca laboratoryjna nr 9. Kryterium Shapiro-Wilka………………43

Praca laboratoryjna nr 10. Kryterium Omega-kwadrat………...47

Praca laboratoryjna nr 11. Kryterium Kołmolgorowa……..…53

Praca laboratoryjna nr 12. Testowanie hipotez

normalność dla wszystkich próbek…………………………………...56

Praca laboratoryjna nr 13. Ocena rodzaju dystrybucji

graficznie……………………………………………………….62

Praca laboratoryjna nr 14. Ocena rodzaju dystrybucji

przez asymetrię i kurtozę…………………………………………………...64

TESTY NIEZAWODNOŚCI…………………………………...66

Praca laboratoryjna nr 15. Definicja wskaźników

wiarygodność według danych eksperymentalnych………………………………………66

Praca laboratoryjna nr 16. Dystrybucja Weibulla

przy obliczaniu wskaźników niezawodności……………………………….…70

Praca laboratoryjna nr 17. rozkłady Rayleigha i

rozkład wykładniczy przy obliczaniu

wskaźniki niezawodności………………………………………………………..72

Praca laboratoryjna nr 18. Planowanie testów

pojedyncza metoda pobierania próbek………………………………………...73

Praca laboratoryjna nr 19. Skrócony plan sekwencyjny

testy niezawodności…………………………………………………………80

BIBLIOGRAFIA…………………………………………………85

Pytania wykładowe:

Wstęp

Modele niezawodnościowe systemów technicznych

Prawa dystrybucji czasu pracy

Wstęp

Ilościowe metody badania obiektów technicznych, zwłaszcza na etapach ich projektowania i tworzenia, zawsze wymagają budowy modeli matematycznych procesów i zjawisk. Model matematyczny jest zwykle rozumiany jako połączony zestaw wyrażeń analitycznych i logicznych oraz warunków początkowych i brzegowych, które z pewnym przybliżeniem odzwierciedlają rzeczywiste procesy funkcjonowania obiektu. Model matematyczny jest informacyjnym odpowiednikiem pełnowymiarowego obiektu, za pomocą którego można uzyskać wiedzę o tworzonym projekcie. Zdolność do przewidywania jest uważana za definiującą właściwość modelu. Wszystko to w pełni odnosi się do matematycznych modeli niezawodności.

Matematyczny model niezawodności rozumiany jest jako taki reprezentowany analitycznie system, który dostarcza pełnej informacji o niezawodności obiektu. Podczas budowania modelu proces zmiany niezawodności w pewien sposób zostaje uproszczony i schematyzowany. Spośród dużej liczby czynników działających na obiekt pełnowymiarowy wyróżnia się główne, których zmiana może powodować zauważalne zmiany niezawodności. Relacje między częściami składowymi systemu mogą być reprezentowane przez zależności analityczne również z pewnymi przybliżeniami. W rezultacie wnioski uzyskane na podstawie badania modelu niezawodności obiektu zawierają pewną niepewność.

Im skuteczniej zostanie wybrany model, tym lepiej odda on charakterystyczne cechy funkcjonowania obiektu, tym dokładniej będzie oceniana jego wiarygodność i uzyskiwane rozsądne rekomendacje do podejmowania decyzji.

1. Modele niezawodnościowe systemów technicznych

Obecnie istnieją ogólne zasady konstruowania matematycznych modeli niezawodności. Model budowany jest tylko dla określonego obiektu, a ściślej dla grupy obiektów tego samego typu, z uwzględnieniem cech ich przyszłej eksploatacji. Musi spełniać następujące wymagania:

Model powinien uwzględniać maksymalną liczbę czynników wpływających na niezawodność obiektu;

Model powinien być na tyle prosty, aby przy użyciu typowych narzędzi obliczeniowych uzyskać wskaźniki niezawodności wyjścia w zależności od zmiany czynników wejściowych.

Niespójność tych wymagań nie pozwala na całkowite sformalizowanie konstrukcji modeli, co czyni proces tworzenia modeli w pewnym stopniu twórczym.

Istnieje wiele klasyfikacji modeli niezawodnościowych, z których jedną pokazano na rysunku 11 .

Rys.1. Klasyfikacja modeli niezawodnościowych

Jak wynika z rys. 1, wszystkie modele można podzielić na dwie duże grupy: modele niezawodności obiektów i modele elementów. Modele niezawodności elementów zawierają więcej treści fizycznych i są bardziej specyficzne dla elementów określonego projektu. Modele te wykorzystują charakterystyki wytrzymałości materiałów, uwzględniają obciążenia działające na konstrukcję, uwzględniają wpływ warunków pracy na pracę elementów. W badaniu tych modeli uzyskuje się sformalizowany opis procesów powstawania uszkodzeń w zależności od wybranych czynników.

Modele niezawodnościowe obiektów są tworzone dla sformalizowanego opisu z punktu widzenia niezawodności procesu ich funkcjonowania jako procesu interakcji elementów składających się na dany obiekt. W takim modelu interakcja elementów odbywa się tylko poprzez najbardziej znaczące połączenia, które wpływają na ogólną niezawodność obiektu.

Istnieją parametryczne modele niezawodności obiektów i modele pod kątem uszkodzeń elementów. Modele parametryczne zawierają funkcje losowych parametrów elementów, co pozwala na uzyskanie pożądanego wskaźnika niezawodności obiektu na wyjściu modelu. Z kolei parametry elementów mogą być funkcjami czasu pracy obiektu.

Modele tworzone pod kątem uszkodzeń elementów są najbardziej sformalizowane i są głównymi w analizie niezawodności złożonych systemów technicznych. Warunkiem koniecznym do stworzenia takich modeli jest jasny opis oznak awarii każdego elementu systemu. Model odzwierciedla wpływ awarii pojedynczego elementu na niezawodność systemu.

Zgodnie z zasadami implementacji modeli różnią się one pod względem analitycznym, statystycznym i kombinowanym (inaczej funkcjonalno – statystycznym).

Modele analityczne zawierają zależności analityczne między parametrami charakteryzującymi niezawodność systemu a wyjściowym wskaźnikiem niezawodności. Aby uzyskać takie zależności, konieczne jest ograniczenie liczby istotnych czynników i znaczne uproszczenie fizycznego obrazu procesu zmiany niezawodności. Dzięki temu modele analityczne mogą z wystarczającą dokładnością opisywać tylko stosunkowo proste problemy zmiany wskaźników niezawodności systemu. Wraz z komplikacją systemu i wzrostem liczby czynników wpływających na niezawodność na pierwszy plan wysuwają się modele statystyczne.

Metoda modelowania statystycznego pozwala na rozwiązywanie problemów wielowymiarowych o dużej złożoności w krótkim czasie iz akceptowalną dokładnością. Wraz z rozwojem technologii komputerowej poszerzają się możliwości tej metody.

Jeszcze większe możliwości ma metoda łączona, która przewiduje tworzenie modeli funkcjonalno-statystycznych. W takich modelach tworzone są modele analityczne dla elementów, a system jako całość modelowany jest w trybie statystycznym.

Wybór jednego lub drugiego modelu matematycznego zależy od celów badania niezawodności obiektu, dostępności wstępnych informacji o niezawodności elementów, znajomości wszystkich czynników wpływających na zmianę niezawodności, gotowości aparatury analitycznej do opisu procesów narastania uszkodzeń i awarii oraz wielu innych przyczyn. Ostatecznie wyboru modelu dokonuje badacz.