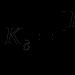Milline järjestustest on monotoonne ja piiratud. Weierstrassi teoreem monotoonse jada piiri kohta. Probleemilahenduse näide

Definitsioon 1. Jada nimetatakse mittekahanevaks [mittekasvavaks], kui jada iga element, alates teisest, ei ole väiksem (mitte suurem kui) selle eelmine element, st kui ebavõrdsus kehtib kõigi arvude puhul.

Definitsioon 2. Jada nimetatakse monotoonseks, kui see on kas mittekahanev või mittekasvav.

Kui kõigi arvude mittekahaneva jada elemendid rahuldavad ranget ebavõrdsust, siis nimetatakse seda jada suurenevaks.

Samamoodi, kui kõigi arvude mittekasvava jada elemendid rahuldavad ranget ebavõrdsust, nimetatakse seda jada kahanevaks.

Pange tähele, et iga monotoonne jada on ühel küljel (kas ülalt või all) piiratud. Tõepoolest, iga mittekahanev jada on allpool piiratud (selle esimese elemendi väärtust võib võtta alumiseks piiriks) ja iga mittekasvav jada on piiratud ülalt (selle esimese elemendi väärtust võib võtta ka ülemiseks piiriks ).

Sellest järeldub, et mittekahanev jada on mõlemalt poolt piiratud või siis lihtsalt piiratud siis ja ainult siis, kui see on ülalpool, ja mittekasvav jada on piiratud siis ja ainult siis, kui see on allpool.

Mõelge monotoonsete järjestuste näidetele.

1. Järjestus on mittekahanev. Altpoolt on see piiratud esimese elemendi väärtusega ja ülalt piiramata.

2. Järjestus väheneb. See on mõlemalt poolt piiratud: ülalt selle esimese elemendi 2 väärtusega ja altpoolt näiteks numbriga 1.

Kui iga naturaalarv n on seotud mõne reaalarvuga x n , siis me ütleme seda numbriline jada

x 1 , x 2 , … x n , …

Number x 1 nimetatakse jada liikmeks numbriga 1 või jada esimene liige, number x 2 - jada liige numbriga 2 või jada teine ​​liige jne. Arvu x n kutsutakse numbriga jada liige n.

Numbriliste jadade määramiseks on kaks võimalust – kasutades ja kasutades korduv valem.

Järjestus koos jada üldtermini valemid on järjestus

x 1 , x 2 , … x n , …

kasutades valemit, mis väljendab liikme x n sõltuvust tema arvust n .

Näide 1. Numbriline jada

1, 4, 9, … n 2 , …

antud üldtermini valemiga

x n = n 2 , n = 1, 2, 3, …

Jada määramist valemiga, mis väljendab jada liiget x n eelnevate numbritega jada liikmetena, nimetatakse sekveneerimiseks kasutades korduv valem.

x 1 , x 2 , … x n , …

helistas kasvav järjestus, rohkem eelmine liige.

Teisisõnu, kõigile n

x n + 1 >x n

Näide 3. Naturaalarvude jada

1, 2, 3, … n, …

on an tõusev järjestus.

Definitsioon 2. Numbrijada

x 1 , x 2 , … x n , …

helistas kahanev järjestus, kui selle jada iga liige vähem eelmine liige.

Teisisõnu, kõigile n= 1, 2, 3, … ebavõrdsus

x n + 1 < x n

Näide 4. Järjestus

antud valemiga

on an kahanev järjestus.

Näide 5 . Numbriline jada

1, - 1, 1, - 1, …

antud valemiga

x n = (- 1) n , n = 1, 2, 3, …

ei ole ei suurene ega kahane järjestus.

Definitsioon 3. Nimetatakse kasvavaid ja kahanevaid arvjadasid monotoonsed jadad.

Piiratud ja piiramata jadad

Definitsioon 4. Numbrijada

x 1 , x 2 , … x n , …

helistas ülalt piiratud kui on olemas selline arv M, et selle jada iga liige vähem numbrid M.

Teisisõnu, kõigile n= 1, 2, 3, … ebavõrdsus

Definitsioon 5. Numbriline jada

x 1 , x 2 , … x n , …

helistas altpoolt piiratud kui on selline arv m, et selle jada iga liige rohkem numbrid m.

Teisisõnu, kõigile n= 1, 2, 3, … ebavõrdsus

Definitsioon 6. Numbrijada

x 1 , x 2 , … x n , …

nimetatakse piiratud, kui see piiratud nii ülalt kui alt.

Teisisõnu on arvud M ja m sellised, et kõigi jaoks n= 1, 2, 3, … ebavõrdsus

m< x n < M

Definitsioon 7. Numbrilised jadad, mis ei ole piiratud, kutsus piiramatud järjestused.

Näide 6. Numbriline jada

1, 4, 9, … n 2 , …

antud valemiga

x n = n 2 , n = 1, 2, 3, … ,

altpoolt piiratud, näiteks arv 0. Kuid see jada piiramatu ülevalt.

Näide 7. Järjestus

antud valemiga

on an piiratud järjestus, sest kõigi jaoks n= 1, 2, 3, … ebavõrdsus

Meie kodulehel saate tutvuda ka Resolventa koolituskeskuse õpetajate väljatöötatud õppematerjalidega matemaatika ühtseks riigieksamiks ja OGE-ks valmistumiseks.

Õpilastele, kes soovivad hästi valmistuda ja läbida KASUTADA matemaatikas või vene keeles kõrge punktisumma eest viib läbi koolituskeskus "Resolventa".

Weierstrassi teoreem monotoonse jada piiri kohta

Mis tahes monotoonselt piiratud jada (x n) mille lõplik piir on võrdne täpse ülemise piiriga, sup (x n) mittekahaneva ja täpse alampiiri jaoks, inf ( x n ) mittekasvava järjestuse jaoks.
Igal monotoonsel piiramata jadal on lõpmatu piir, mis on võrdne pluss lõpmatusega mittekahaneva jada puhul ja miinus lõpmatusega mittekasvava jada puhul.

Tõestus

1) mittekahanev piiratud järjestus.

(1.1) .

Kuna jada on piiratud, on sellel lõplik täpne ülemine piir
.
See tähendab et:

• kõigi n jaoks,
  (1.2) ;
• iga positiivse arvu korral on ε-st sõltuv arv, nii et
  (1.3) .

.
Siin kasutasime ka (1.3). Kombineerides (1.2) leiame:
aadressil .
Sest siis
,
või
aadressil .
Teoreemi esimene osa on tõestatud.

2) Nüüd las jada olla mittekasvav piiratud jada:
(2.1) kõigile n.

Kuna jada on piiratud, on sellel lõplik täpne alumine piir
.
See tähendab järgmist:

• kõigi n-i puhul kehtivad järgmised ebavõrdsused:
  (2.2) ;
• iga positiivse arvu korral on arv, mis sõltub ε-st, mille jaoks
  (2.3) .

.
Siin kasutasime ka (2.3). Võttes arvesse punkti (2.2), leiame:
aadressil .
Sest siis
,
või
aadressil .
See tähendab, et arv on jada piir.
Teoreemi teine ​​osa on tõestatud.

Nüüd kaaluge piiramata jadasid.
3) Las jada olla piiramatu mittekahanev järjestus.

Kuna jada on mittekahanev, kehtivad järgmised ebavõrdsused kõigi n-de kohta:
(3.1) .

Kuna jada on mittekahanev ja piiramatu, on see paremal pool piiramatu. Siis on mis tahes arvu M jaoks olemas arv, mis sõltub M-st, mille jaoks
(3.2) .

Kuna järjestus on mittekahanev, siis meil on:
.
Siin kasutasime ka (3.2).

.
See tähendab, et jada piir on pluss lõpmatus:
.
Teoreemi kolmas osa on tõestatud.

4) Lõpuks mõelge juhtumile, kui piiramatu mittesuurenev järjestus.

Nagu eespool, kuna järjestus ei kasva, siis
(4.1) kõigile n.

Kuna jada on mittekasvav ja piiramatu, on see vasakul pool piiramatu. Siis on mis tahes arvu M jaoks olemas arv, mis sõltub M-st, mille jaoks
(4.2) .

Kuna järjestus ei kasva, siis meil on:
.

Seega on mis tahes arvu M jaoks olemas naturaalarv, mis sõltub M-st, nii et järgmised ebavõrdsused kehtivad kõigi arvude kohta:
.
See tähendab, et jada piir on miinus lõpmatus:
.
Teoreem on tõestatud.

Probleemilahenduse näide

Kasutades Weierstrassi teoreemi, tõestage jada konvergents:
, , . . . , , . . .
Seejärel leidke oma piir.

Esitame jada korduvate valemite kujul:
,
.

Tõestame, et antud jada on ülalt piiratud väärtusega
(P1) .
Tõestus viiakse läbi matemaatilise induktsiooni meetodil.
.
Laske . Siis
.
Ebavõrdsus (A1) on tõestatud.

Tõestame, et jada kasvab monotoonselt.
;
(P2) .
Kuna , siis on murdosa nimetaja ja lugeja esimene tegur positiivsed. Kuna jada liikmed on piiratud ebavõrdsusega (P1), on ka teine ​​tegur positiivne. Niisiis
.
See tähendab, et järjestus suureneb rangelt.

Kuna jada kasvab ja on ülalt piiratud, on see piiratud jada. Seetõttu on sellel Weierstrassi teoreemi kohaselt piir.

Leiame selle piiri. Tähistame seda tähega:
.
Kasutame mida
.
Rakendame seda (P2) jaoks, kasutades konvergentsete jadade piiride aritmeetilisi omadusi:
.
Juur rahuldab tingimust.

Definitsioon. Nimetatakse jada (x n ). piiratud, kui on selline arv M>0, et mis tahes n tõeline ebavõrdsus:

need. kõik jada liikmed kuuluvad intervalli (-M; M).

Näiteks jadad 2 0), 3 0), 4 0), 5 0) on piiratud, samas kui jada 1 0) on piiramata.

Piiratud jada definitsioonist ja jada piiri definitsioonist tuleneb otseselt järgmine teoreem:

Teoreem. Kui x n ® a, siis jada (x n ) on piiratud.

Tuleb märkida, et vastupidine väide ei vasta tõele, s.t. jada piiritus ei tähenda selle konvergentsi.

Näiteks järjestus piiranguid siiski pole

Definitsioon. Nimetatakse jada (x n ). ülalt piiratud, kui üldse n on olemas arv M, mille puhul x n £ M.

Näide.(x n ) \u003d 3n - altpoolt piiratud (3, 6, 9, ... ).

monotoonsed jadad.

Definitsioon. 1) Kui x n +1 > x n kõigi n puhul, siis jada kasvab.

2) Kui x n +1 ³ x n kõigi n puhul, siis on jada mittekahanev.

3) Kui x n +1< x n для всех n, то последовательность убывающая.

4) Kui x n +1 £ x n kõigi n puhul, siis jada ei kasva

Kõiki neid jadasid nimetatakse üksluine. Kasvavaid ja kahanevaid jadasid nimetatakse rangelt monotoonne.

Näide.(x n ) = 1/n – kahanev ja piiratud

(x n ) = n – kasvav ja piiramatu.

Näide. Tõesta, et jada (x n )= on monotoonne kasvav.

Lahendus. Leidke jada liige (x n +1 )=

Leia erinevuse märk: (x n )-(x n +1 )=

, sest nнN, siis on nimetaja iga n puhul positiivne.

Seega x n +1 > x n . Järjestus suureneb, mida tuleks tõestada.

Näide. Uurige, kas jada on tõusev või kahanev

Lahendus. Otsime üles. Leiame erinevuse

Sest nОN, siis 1 – 4n<0, т.е. х n+1 < x n . Последовательность монотонно убывает.

Tuleb märkida, et monotoonsed järjestused on vähemalt ühelt poolt piiratud.

Teoreem. Monotoonse piiriga jadal on piir.

Tõestus. Mõelge monotoonsele mittekahanevale jadale

x 1 £ x 2 £ x 3 £ ... £ x n £ x n +1 £ ...

See jada on ülalt piiratud: x n £ M, kus M on mingi arv.

Sest igal ülalt piiritletud arvulisel hulgal on selge ülempiir, siis iga e>0 jaoks on olemas arv N, mille puhul x N > a - e, kus a on mingi hulga ülempiir.

Sest (x n ) on mittekahanev jada, siis N > n a - e korral< x N £ x n ,

Siit a - e< x n < a + e

E< x n – a < e или ôx n - aô< e, т.е. lim x n = a.

Teiste monotoonsete jadade puhul on tõestus sarnane.

Teoreem on tõestatud.

§3. Number e.

Vaatleme jada (x n ) = .

Kui jada (x n ) on monotoonne ja piiratud, siis on sellel lõplik piir.

Newtoni binoomvalemi järgi:

Või mis on sama

Näitame, et jada (x n ) kasvab. Tõepoolest, kirjutame avaldise x n +1 ja võrdleme seda avaldisega x n:

Avaldise x n +1 iga liige on suurem kui vastav x n väärtus ja lisaks on x n +1-le lisatud veel üks positiivne liige. Seega jada (x n ) kasvab.

Tõestame nüüd, et ühegi n korral ei ületa selle liikmed kolme: x n< 3.

Niisiis, jada on monotoonselt kasvav ja ülalt piiratud, st. on piiratud piir. Seda piiri tähistatakse tavaliselt tähega e.

Ebavõrdsusest järeldub, et e £ 3. Jättes kõrvale (x n) kõik liikmed, alates neljandast, saame:

ületades piiri, saame

Seega on arv e arvude 2,5 ja 3 vahel. Kui võtta reas suurem arv liikmeid, siis saame arvu e väärtusele täpsema hinnangu.

Võib näidata, et arv e on irratsionaalne ja selle väärtus on 2,71828 ...

Samamoodi võib seda näidata , laiendades x-i nõudeid mis tahes reaalarvuni:

Oletame:

Arv e on naturaallogaritmi alus.

Ülal on funktsiooni y = lnx graafik.

Naturaal- ja kümnendlogaritmide vaheline seos.

Olgu x \u003d 10 y, siis lnx \u003d ln10 y, seega lnx \u003d yln10

y = , kus M = 1/ln10 » 0,43429… on üleminekumoodul.

§4. Funktsiooni piiri mõiste.

4.1. Funktsiooni piirväärtus punktis.

y f(x)

0 a - D a a + D x

Olgu funktsioon f(x) defineeritud punkti x = a mõnes naabruses (st punktis x = a ise ei pruugi funktsioon olla defineeritud)

Definitsioon. Kutsutakse numbrit A piir funktsioon f(x) x®a jaoks, kui mis tahes e>0 korral on olemas arv D>0, nii et kõigi x-ide korral

ix - ai< D

ebavõrdsus ïf(x) - Aï< e.

Sama määratluse saab kirjutada erineval kujul:

Kui a - D< x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Funktsiooni piiri kirjutamine punktis:

Põhiteoreemid piiride kohta.

1. teoreem. , kus C = konst.

Järgmised teoreemid kehtivad eeldusel, et funktsioonidel f(x) ja g(x) on lõplikud piirid kui x®a.

2. teoreem.

Selle teoreemi tõestus esitatakse allpool.

3. teoreem.

Tagajärg.

4. teoreem. juures

5. teoreem. Kui f(x)>0 punkti lähedal x = a ja , siis A>0.

f(x) piirmärk< 0, f(x) ³ 0, f(x) £ 0.

6. teoreem. Kui g(x) £ f(x) £ u(x) punkti x lähedal = a ja , siis ja .

Definitsioon. Kutsutakse funktsioon f(x). piiratud punkti x = a lähedal, kui on olemas arv M>0, et ïf(x)ï

7. teoreem. Kui funktsioonil f(x) on lõplik piir nagu x®a, siis on see piiratud punkti x = a lähedal.

Tõestus. Lase , s.t. , siis

Kus M \u003d e + ïAi

Teoreem on tõestatud.

4.2. Ühepoolsed piirangud.

Definitsioon. Kui f(x) ® A 1 x ® a jaoks on ainult x< a, то - называется piir funktsioon f(x) punktis x = a vasakule, ja kui f(x) ® A 2 x ® a jaoks on ainult x > a, siis helistas piir funktsioon f(x) punktis x = a paremal.

juures

Ülaltoodud definitsioon viitab juhule, kui funktsioon f(x) ei ole defineeritud punktis x = a ise, vaid on defineeritud selle punkti mõnes suvaliselt väikeses ümbruses.

Nimetatakse ka piirväärtusi A 1 ja A 2 ühepoolsed piirangud funktsioonid f(x) punktis x = a. Samuti räägitakse, et A lõplik piir funktsioonid f(x).

4.3.Funktsiooni piir, kui argument kaldub lõpmatuseni.

Definitsioon. Kutsutakse numbrit A piir funktsioon f(x) x®¥ jaoks, kui mis tahes arvu e>0 korral on olemas arv M>0, nii et kõigi x, ïxï>M korral on ebavõrdsus