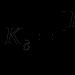Ardıcıllıqlardan hansı monoton və məhduddur. Monoton ardıcıllığın həddi haqqında Weierstrass teoremi. Problem həlli nümunəsi

Tərif 1. Əgər ardıcıllığın hər bir elementi ikincidən başlayaraq əvvəlki elementindən az (çox deyil) deyilsə, yəni bərabərsizlik bütün ədədlər üçün doğrudursa, ardıcıllıqla azalmayan [artan olmayan] adlanır.

Tərif 2. Ardıcıllıq azalmayan və ya artmayan olduqda monoton adlanır.

Bütün ədədlər üçün azalmayan ardıcıllığın elementləri ciddi bərabərsizliyi ödəyirsə, bu ardıcıllığa artan deyilir.

Eynilə, bütün ədədlər üçün artan olmayan ardıcıllığın elementləri ciddi bərabərsizliyi ödəyirsə, bu ardıcıllığa azalan deyilir.

Qeyd edək ki, hər bir monoton ardıcıllıq bir tərəfdən (yuxarıda və ya aşağıda) məhduddur. Həqiqətən, hər bir azalmayan ardıcıllıq aşağıda məhduddur (onun ilk elementinin dəyəri aşağı hədd kimi qəbul edilə bilər) və hər bir artmayan ardıcıllıq yuxarıda məhduddur (onun birinci elementinin dəyəri də yuxarı həddi kimi qəbul edilə bilər) ).

Buradan belə nəticə çıxır ki, azalmayan ardıcıllıq hər iki tərəfdən məhdudlaşacaq və ya sadəcə yuxarıdan məhdudlaşdığı təqdirdə məhdudlaşacaq, artan olmayan ardıcıllıq isə yalnız və yalnız aşağıdan məhdudlaşdığı halda məhdudlaşacaq.

Monoton ardıcıllıq nümunələrini nəzərdən keçirin.

1. Ardıcıllıq azalan deyil. O, ilk elementinin dəyəri ilə aşağıda məhdudlaşır, yuxarıda isə qeyri-məhduddur.

2. Ardıcıllıq azalır. Hər iki tərəfdən məhduddur: yuxarıdan onun ilk elementinin 2 dəyəri ilə və aşağıdan, məsələn, 1 nömrəsi ilə.

Əgər hər bir n natural ədədi hansısa həqiqi x n ədədi ilə əlaqələndirilirsə, biz bunu deyirik ədədi ardıcıllıq

x 1 , x 2 , … x n , …

Nömrə x 1 ardıcıllığın üzvü adlanır 1 nömrəsi ilə və ya ardıcıllığın ilk üzvü, nömrə x 2 - ardıcıllıq üzvü 2 nömrəsi ilə və ya ardıcıllığın ikinci üzvü və s. x n ədədi adlanır nömrə ilə ardıcıllığın üzvü n.

Ədədi ardıcıllığı təyin etməyin iki yolu var - istifadə və istifadə təkrarlanan formula.

ilə ardıcıllıqla ardıcıllıq ümumi termin düsturları ardıcıllıqdır

x 1 , x 2 , … x n , …

x n üzvünün n sayından asılılığını ifadə edən düsturdan istifadə etməklə.

Nümunə 1. Rəqəmsal ardıcıllıq

1, 4, 9, … n 2 , …

ümumi termin düsturu ilə verilir

x n = n 2 , n = 1, 2, 3, …

Əvvəlki nömrələrlə ardıcıllıq üzvləri baxımından x n ardıcıllıq üzvünü ifadə edən düsturdan istifadə edərək ardıcıllığın təyin edilməsinə ardıcıllıq deyilir. təkrarlanan formula.

x 1 , x 2 , … x n , …

çağırdı artan ardıcıllıqla, daha çoxəvvəlki üzv.

Başqa sözlə, hər kəs üçün n

x n + 1 >x n

Misal 3. Natural ədədlərin ardıcıllığı

1, 2, 3, … n, …

bir artan ardıcıllıq.

Tərif 2. Say ardıcıllığı

x 1 , x 2 , … x n , …

çağırdı enən ardıcıllıq,əgər bu ardıcıllığın hər bir üzvü azəvvəlki üzv.

Başqa sözlə, hər kəs üçün n= 1, 2, 3, … bərabərsizlik

x n + 1 < x n

Misal 4. Ardıcıllıq

düsturla verilir

bir enən ardıcıllıq.

Misal 5. Rəqəmsal ardıcıllıq

1, - 1, 1, - 1, …

düsturla verilir

x n = (- 1) n , n = 1, 2, 3, …

deyil nə artır, nə də azalır ardıcıllıq.

Tərif 3. Artan və azalan ədədi ardıcıllıqlar deyilir monoton ardıcıllıqlar.

Məhdud və məhdudiyyətsiz ardıcıllıqlar

Tərif 4. Say ardıcıllığı

x 1 , x 2 , … x n , …

çağırdı yuxarıdan məhduddurəgər bu ardıcıllığın hər bir üzvü M ədədi varsa az nömrələr M.

Başqa sözlə, hər kəs üçün n= 1, 2, 3, … bərabərsizlik

Tərif 5. Ədədi ardıcıllıq

x 1 , x 2 , … x n , …

çağırdı aşağıdan məhdudlaşdırılırəgər bu ardıcıllığın hər bir üzvü belə m ədədi varsa daha çox nömrələr m.

Başqa sözlə, hər kəs üçün n= 1, 2, 3, … bərabərsizlik

Tərif 6. Say ardıcıllığı

x 1 , x 2 , … x n , …

əgər məhdud adlanır həm yuxarıda, həm də aşağıda məhdudlaşır.

Başqa sözlə, M və m rəqəmləri var ki, hamı üçün n= 1, 2, 3, … bərabərsizlik

m< x n < M

Tərif 7. Ədədi ardıcıllıqlar ki məhdud deyil, çağırdı limitsiz ardıcıllıq.

Misal 6. Rəqəmsal ardıcıllıq

1, 4, 9, … n 2 , …

düsturla verilir

x n = n 2 , n = 1, 2, 3, … ,

aşağıdan məhdudlaşdırılır məsələn, 0 rəqəmi. Lakin bu ardıcıllıq yuxarıdan qeyri-məhdud.

Misal 7. Ardıcıllıq

düsturla verilir

bir məhdud ardıcıllıq, çünki hamı üçün n= 1, 2, 3, … bərabərsizlik

Veb saytımızda siz Resolventa tədris mərkəzinin müəllimləri tərəfindən Vahid Dövlət İmtahanına və riyaziyyat üzrə OGE-yə hazırlaşmaq üçün hazırlanmış tədris materialları ilə də tanış ola bilərsiniz.

Yaxşı hazırlaşıb keçmək istəyən tələbələr üçün riyaziyyat və ya rus dilində İSTİFADƏ yüksək bal üçün "Resolventa" təlim mərkəzi aparır

Monoton ardıcıllığın həddi haqqında Weierstrass teoremi

İstənilən monoton məhdud ardıcıllıq ( x n ) dəqiq yuxarı həddə bərabər sonlu həddi var, sup ( x n ) azalmayan və dəqiq aşağı hədd üçün, inf ( x n ) artan olmayan ardıcıllıq üçün.
İstənilən monotonik qeyri-məhdud ardıcıllığın sonsuz həddi azalmayan ardıcıllıq üçün plus sonsuzluğa, artmayan ardıcıllıq üçün isə mənfi sonsuzluğa bərabərdir.

Sübut

1) azalmayan məhdud ardıcıllıq.

(1.1) .

Ardıcıllıq məhdud olduğundan, onun sonlu dəqiq yuxarı sərhədi var
.
Bu o deməkdir ki:

• bütün n üçün,
  (1.2) ;
• hər hansı müsbət ədəd üçün ε-dən asılı olan ədəd var, belə ki
  (1.3) .

.
Burada da (1.3) istifadə etdik. (1.2) ilə birləşdirərək tapırıq:
at.
O vaxtdan bəri
,
və ya
at.
Teoremin birinci hissəsi sübut edilmişdir.

2) İndi ardıcıllıq olsun artan olmayan məhdud ardıcıllıq:
(2.1) hamı üçün n.

Ardıcıllıq məhdud olduğundan, sonlu dəqiq aşağı sərhədə malikdir
.
Bu, aşağıdakılar deməkdir:

• bütün n üçün aşağıdakı bərabərsizliklər yerinə yetirilir:
  (2.2) ;
• hər hansı müsbət ədəd üçün ε-dən asılı olaraq bir ədəd var
  (2.3) .

.
Burada da (2.3) istifadə etdik. (2.2) nəzərə alaraq biz tapırıq:
at.
O vaxtdan bəri
,
və ya
at.
Bu o deməkdir ki, nömrə ardıcıllığın həddidir.
Teoremin ikinci hissəsi sübut edilmişdir.

İndi qeyri-məhdud ardıcıllıqları nəzərdən keçirin.
3) Ardıcıllıq olsun limitsiz azalmayan ardıcıllıq.

Ardıcıllıq azalmayan olduğundan, bütün n üçün aşağıdakı bərabərsizliklər yerinə yetirilir:
(3.1) .

Ardıcıllıq azalmayan və qeyri-məhdud olduğu üçün sağ tərəfdə sərhədsizdir. Onda hər hansı M ədədi üçün M-dən asılı olaraq bir ədəd mövcuddur
(3.2) .

Ardıcıllıq azalmayan olduğundan, bizim üçün:
.
Burada da (3.2) istifadə etdik.

.
Bu o deməkdir ki, ardıcıllığın limiti üstəgəl sonsuzdur:
.
Teoremin üçüncü hissəsi sübut edilmişdir.

4) Nəhayət, nə vaxt olduğunu düşünün limitsiz artan olmayan ardıcıllıq.

Yuxarıda göstərildiyi kimi, ardıcıllıq artan olmadığı üçün
(4.1) hamı üçün n.

Ardıcıllıq artan və qeyri-məhdud olduğu üçün sol tərəfdə sərhədsizdir. Onda hər hansı M ədədi üçün M-dən asılı olaraq bir ədəd mövcuddur
(4.2) .

Ardıcıllıq artan olmadığı üçün bizdə:
.

Beləliklə, hər hansı M ədədi üçün M-dən asılı olan bir natural ədəd var ki, bərabərsizliklər bütün ədədlər üçün olsun:
.
Bu o deməkdir ki, ardıcıllığın limiti mənfi sonsuzdur:
.
Teorem sübut edilmişdir.

Problem həlli nümunəsi

Weierstrass teoremindən istifadə edərək ardıcıllığın yaxınlaşmasını sübut edin:
, , . . . , , . . .
Sonra onun həddini tapın.

Ardıcıllığı təkrarlanan düsturlar şəklində təqdim edək:
,
.

Verilmiş ardıcıllığın yuxarıdan qiymətlə məhdudlaşdığını sübut edək
(P1) .
Sübut riyazi induksiya üsulu ilə həyata keçirilir.
.
Qoy . Sonra
.
Bərabərsizlik (A1) sübut edilmişdir.

Ardıcıllığın monoton şəkildə artdığını sübut edək.
;
(P2) .
-dən bəri kəsrin məxrəci və paydakı birinci amili müsbətdir. Ardıcıllığın şərtləri bərabərsizlik (P1) ilə məhdudlaşdığından ikinci amil də müsbətdir. Belə ki
.
Yəni ardıcıllıq ciddi şəkildə artır.

Ardıcıllıq yuxarıdan artan və məhdud olduğu üçün məhdud ardıcıllıqdır. Beləliklə, Weierstrass teoreminə görə, onun bir həddi var.

Gəlin bu həddi tapaq. Bunu ilə işarə edək:
.
Nə istifadə edək
.
Konvergent ardıcıllıqların hədlərinin arifmetik xüsusiyyətlərindən istifadə edərək bunu (P2) tətbiq edirik:
.
Kök şərti təmin edir.

Tərif. Ardıcıllığa (x n ) deyilir məhduddur, əgər belə bir ədəd M>0 olarsa ki, hər hansı üçün n həqiqi bərabərsizlik:

olanlar. ardıcıllığın bütün üzvləri (-M; M) intervalına aiddir.

Məsələn, 2 0), 3 0), 4 0), 5 0) ardıcıllıqları məhduddur, 1 0) ardıcıllığı isə qeyri-məhduddur.

Aşağıdakı teorem birbaşa məhdud ardıcıllığın tərifindən və ardıcıllığın limitinin tərifindən irəli gəlir:

teorem. Əgər x n ® a olarsa, onda ardıcıllıq (x n ) məhduddur.

Qeyd etmək lazımdır ki, əks ifadə doğru deyil, yəni. ardıcıllığın məhdudluğu onun yaxınlaşmasını nəzərdə tutmur.

Məsələn, ardıcıllıq baxmayaraq ki, limit yoxdur

Tərif. Ardıcıllığa (x n ) deyilir yuxarıdan məhdudlaşır, əgər varsa n x n £ M olan bir M ədədi mövcuddur.

Misal.(x n ) \u003d 3n - aşağıdan məhdudlaşır (3, 6, 9, ... ).

monoton ardıcıllıqlar.

Tərif. 1) Bütün n üçün x n +1 > x n olarsa, ardıcıllıq artır.

2) Bütün n üçün x n +1 ³ x n olarsa, ardıcıllıq azalmır.

3) Əgər x n +1 olarsa< x n для всех n, то последовательность убывающая.

4) Əgər bütün n üçün x n +1 £ x n olarsa, ardıcıllıq artan deyildir.

Bütün bu ardıcıllıqlar deyilir monoton. Artan və azalan ardıcıllıqlar deyilir ciddi monoton.

Misal.(x n ) = 1/n - azalan və məhduddur

(x n ) = n - artan və qeyri-məhdud.

Misal.(x n )= ardıcıllığının monoton artan olduğunu sübut edin.

Həll.(x n +1 )= ardıcıllığının üzvünü tapın

Fərqin işarəsini tapın: (x n )-(x n +1 )=

, çünki nнN, onda məxrəc istənilən n üçün müsbətdir.

Beləliklə, x n +1 > x n . Ardıcıllıq artır, bunu sübut etmək lazımdır.

Misal. Ardıcıllığın artan və ya azalan olduğunu öyrənin

Həll. tapaq. Gəlin fərqi tapaq

Çünki nОN, sonra 1 - 4n<0, т.е. х n+1 < x n . Последовательность монотонно убывает.

Qeyd etmək lazımdır ki, monotonik ardıcıllıqlar ən azı bir tərəfdən məhduddur.

teorem. Monoton məhdud ardıcıllığın limiti var.

Sübut. Monoton azalmayan ardıcıllığı nəzərdən keçirək

x 1 £ x 2 £ x 3 £ ... £ x n £ x n +1 £ ...

Bu ardıcıllıq yuxarıdan məhduddur: x n £ M, burada M hansısa ədəddir.

Çünki yuxarıdan məhdud olan istənilən ədədi çoxluğun aydın yuxarı həddi var, onda hər hansı e>0 üçün N ədədi var ki, x N > a - e, burada a çoxluğun yuxarı sərhəddidir.

Çünki (x n ) azalmayan ardıcıllıqdır, onda N > n a - e üçün< x N £ x n ,

Buradan a - e< x n < a + e

E< x n – a < e или ôx n - aô< e, т.е. lim x n = a.

Digər monoton ardıcıllıqlar üçün sübut oxşardır.

Teorem sübut edilmişdir.

§3. Nömrə e.

(x n ) = ardıcıllığını nəzərdən keçirək.

Ardıcıllıq (x n ) monotondursa və məhduddursa, onun sonlu həddi var.

Nyutonun binom düsturuna görə:

Və ya eyni nədir

(x n ) ardıcıllığının artdığını göstərək. Doğrudan da, x n +1 ifadəsini yazaq və onu x n ifadəsi ilə müqayisə edək:

x n +1 ifadəsindəki hər bir termin x n -nin müvafiq qiymətindən böyükdür və əlavə olaraq, x n +1-ə daha bir müsbət hədd əlavə olunur. Beləliklə, ardıcıllıq (x n ) artır.

İndi sübut edək ki, hər hansı n üçün onun şərtləri üçdən çox deyil: x n< 3.

Beləliklə, ardıcıllıq monoton şəkildə artır və yuxarıdan məhdudlaşır, yəni. sonlu həddi var. Bu hədd adətən hərflə işarələnir e.

Bərabərsizlikdən belə nəticə çıxır ki, e £ 3. Dördüncüdən başlayaraq bütün şərtlər üçün (x n) bərabərliyindən imtina etsək:

həddi keçərək alırıq

Beləliklə, e rəqəmi 2,5 və 3 ədədləri arasındadır.Serialda daha çox sayda termin götürsək, o zaman e ədədinin qiymətinin daha dəqiq qiymətləndirilməsini əldə edə bilərik.

Göstərilə bilər ki, e rəqəmi irrasionaldır və onun dəyəri 2,71828 ...

Eynilə, bunu göstərmək olar , x üçün tələbləri istənilən real ədədə genişləndirərək:

Güman:

e ədədi natural loqarifmin əsasını təşkil edir.

Yuxarıda y = lnx funksiyasının qrafiki verilmişdir.

Natural və onluq loqarifmlər arasında əlaqə.

Qoy x \u003d 10 y, sonra lnx \u003d ln10 y, buna görə də lnx \u003d yln10

y =, burada M = 1/ln10 » 0,43429… keçid moduludur.

§4. Funksiya həddi anlayışı.

4.1. Bir nöqtədə funksiyanın limiti.

y f(x)

0 a - D a a + D x

f(x) funksiyası x = a nöqtəsinin hansısa qonşuluğunda müəyyən edilsin (yəni x = a nöqtəsinin özündə funksiya təyin olunmaya bilər)

Tərif. A nömrəsi deyilir limit x®a üçün f(x) funksiyası, əgər hər hansı e>0 üçün D>0 ədədi mövcuddur ki, bütün x üçün belə

ix - ai< D

ïf(x) bərabərsizliyi - Aï< e.

Eyni tərif başqa formada da yazıla bilər:

Əgər a - D< x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Bir nöqtədə funksiyanın limitinin yazılması:

Limitlər haqqında əsas teoremlər.

Teorem 1. , burada C = const.

Aşağıdakı teoremlər f(x) və g(x) funksiyalarının x®a kimi sonlu hədləri olduğu fərziyyəsi ilə etibarlıdır.

Teorem 2.

Bu teoremin sübutu aşağıda veriləcəkdir.

Teorem 3.

Nəticə.

Teorem 4. saat

Teorem 5. Əgər x = a və nöqtəsinin yaxınlığında f(x)>0 olarsa, onda A>0.

f(x) üçün limit işarəsi< 0, f(x) ³ 0, f(x) £ 0.

Teorem 6. Əgər g(x) £ f(x) £ u(x) x nöqtəsinə yaxın olarsa = a və , sonra və .

Tərif. f(x) funksiyası çağırılır məhduddur x = a nöqtəsinin yaxınlığında ïf(x)ï olan M>0 ədədi varsa

Teorem 7. Əgər f(x) funksiyasının x®a kimi sonlu həddi varsa, o zaman x = a nöqtəsinin yaxınlığında məhdudlaşır.

Sübut. Qoy, yəni. , sonra

Harada M \u003d e + ïAi

Teorem sübut edilmişdir.

4.2. Birtərəfli məhdudiyyətlər.

Tərif. Əgər f(x) ® A 1 x üçün ® a yalnız x üçün< a, то - называется limit x = a nöqtəsində f(x) funksiyası sol, və əgər f(x) ® A 2 üçün x ® a yalnız x > a üçün olarsa, onda çağırdı limit x = a nöqtəsində f(x) funksiyası sağda.

saat

Yuxarıdakı tərif f(x) funksiyasının özü x = a nöqtəsində müəyyən edilmədiyi, lakin bu nöqtənin bəzi ixtiyari kiçik qonşuluğunda müəyyən edildiyi vəziyyətə aiddir.

A 1 və A 2 limitləri də adlanır birtərəfli məhdudiyyətlər x = a nöqtəsində f(x) funksiyaları. Həmçinin bildirilir ki, Ə son hədd f(x) funksiyaları.

4.3.Arqument sonsuzluğa meyl etdikdə funksiyanın limiti.

Tərif. A nömrəsi deyilir limit x®¥ üçün f(x) funksiyası, əgər hər hansı e>0 ədədi üçün M>0 ədədi mövcuddur ki, bütün x, ïxï>M üçün bərabərsizlik olsun