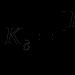1. Układy równań liniowych z parametrem

Układy równań liniowych z parametrem rozwiązuje się tymi samymi podstawowymi metodami, co konwencjonalne układy równań: metodą podstawienia, metodą dodawania równań i metodą graficzną. Znajomość interpretacji graficznej układów liniowych ułatwia odpowiedź na pytanie o liczbę pierwiastków i ich istnienie.

Przykład 1

Znajdź wszystkie wartości parametru a, dla którego układ równań nie ma rozwiązań.

(x + (a 2 - 3) y \u003d a,
(x + y = 2.

Rozwiązanie.

Przyjrzyjmy się kilku sposobom rozwiązania tego problemu.

1 sposób. Korzystamy z własności: układ nie ma rozwiązań, jeśli stosunek współczynników przed x jest równy stosunkowi współczynników przed y, ale nie jest równy stosunkowi wyrazów swobodnych (a/a 1 = b/ b 1 ≠ c/c 1). Następnie mamy:

1/1 \u003d (a 2 - 3) / 1 ≠ a / 2 lub system

(i 2 - 3 = 1,
(a 2.

Dlatego z pierwszego równania a 2 \u003d 4, biorąc pod uwagę warunek, że ≠ 2, otrzymujemy odpowiedź.

Odpowiedź: a = -2.

2 sposób. Rozwiązujemy metodą substytucyjną.

(2 - y + (a 2 - 3) y \u003d a,
(x = 2 - y,

((a 2 - 3) y - y \u003d a - 2,
(x = 2 - y.

Po wyjęciu wspólnego dzielnika y z nawiasów w pierwszym równaniu otrzymujemy:

((a 2 - 4) y \u003d a - 2,
(x = 2 - y.

Układ nie ma rozwiązań, jeśli pierwsze równanie nie ma rozwiązań, czyli

(i 2 - 4 = 0,
(a - 2 ≠ 0.

Jest oczywiste, że a = ±2, ale biorąc pod uwagę drugi warunek, podana jest tylko odpowiedź z minusem.

Odpowiedź: a = -2.

Przykład 2

Znajdź wszystkie wartości parametru a, dla którego układ równań ma nieskończoną liczbę rozwiązań.

(8x + ay = 2,
(topór + 2 lata = 1.

Rozwiązanie.

Według właściwości, jeśli stosunek współczynników przy x i y jest taki sam i jest równy stosunkowi wolnych członków systemu, wówczas ma nieskończoną liczbę rozwiązań (tj. a / a 1 \u003d b / b 1 \u003d c / c 1). Stąd 8/a = a/2 = 2/1. Rozwiązując każde z uzyskanych równań, stwierdzamy, że \u003d 4 jest odpowiedzią w tym przykładzie.

Odpowiedź: a = 4.

2. Układy równań wymiernych z parametrem

Przykład 3

(3|x| + y = 2,
(|x| + 2y = a.

Rozwiązanie.

Pomnóż pierwsze równanie układu przez 2:

(6|x| + 2y = 4,
(|x| + 2y = a.

Odejmij drugie równanie od pierwszego, otrzymamy 5|х| = 4 – a. To równanie będzie miało unikalne rozwiązanie dla a = 4. W innych przypadkach to równanie będzie miało dwa rozwiązania (dla a< 4) или ни одного (при а > 4).

Odpowiedź: a = 4.

Przykład 4

Znajdź wszystkie wartości parametru a, dla którego układ równań ma unikalne rozwiązanie.

(x + y = a,
(y - x 2 \u003d 1.

Rozwiązanie.

Rozwiążemy ten system metodą graficzną. Tak więc wykres drugiego równania układu jest parabolą podniesioną wzdłuż osi Oy o jeden segment jednostkowy. Pierwsze równanie definiuje zbiór linii równoległych do prostej y = -x (obrazek 1). Rysunek wyraźnie pokazuje, że układ ma rozwiązanie, jeśli prosta y = -x + a jest styczna do paraboli w punkcie o współrzędnych (-0,5; 1,25). Podstawiając te współrzędne zamiast x i y do równania, znajdujemy wartość parametru a:

1,25 = 0,5 + a;

Odpowiedź: a = 0,75.

Przykład 5

Korzystając z metody substytucji, dowiedz się, przy jakiej wartości parametru a, system ma unikalne rozwiązanie.

(ax - y \u003d a + 1,
(ax + (a + 2)y = 2.

Rozwiązanie.

Wyraź y z pierwszego równania i zastąp je drugim:

(y \u003d ah - a - 1,
(topór + (a + 2) (topór - a - 1) = 2.

Drugie równanie sprowadzamy do postaci kx = b, która będzie miała jednoznaczne rozwiązanie dla k ≠ 0. Mamy:

topór + a 2 x - a 2 - a + 2ax - 2a - 2 \u003d 2;

a 2 x + 3ax \u003d 2 + a 2 + 3a + 2.

Trójmian kwadratowy a 2 + 3a + 2 można przedstawić jako iloczyn nawiasów

(a + 2)(a + 1), a po lewej wyciągamy x z nawiasów:

(a 2 + 3a) x \u003d 2 + (a + 2) (a + 1).

Oczywiście 2 + 3a nie może być równe zeru, dlatego

a 2 + 3a ≠ 0, a(a + 3) ≠ 0, co oznacza a ≠ 0 i ≠ -3.

Odpowiedź: a 0; -3.

Przykład 6

Korzystając z metody rozwiązania graficznego określ, przy jakiej wartości parametru a, system posiada unikalne rozwiązanie.

(x 2 + y 2 = 9,
(y - |x| = a.

Rozwiązanie.

Na podstawie warunku budujemy okrąg ze środkiem na początku współrzędnych i promieniem 3 jednostkowych odcinków, to ten okrąg wyznacza pierwsze równanie układu

x 2 + y 2 = 9. Drugie równanie układu (y = |x| + a) jest linią łamaną. Przez Rysunek 2 rozważamy wszystkie możliwe przypadki jego położenia względem okręgu. Łatwo zauważyć, że a = 3.

Odpowiedź: a = 3.

Czy masz jakieś pytania? Nie wiesz, jak rozwiązywać układy równań?
Aby uzyskać pomoc od korepetytora -.
Pierwsza lekcja jest bezpłatna!

blog.site, z pełnym lub częściowym skopiowaniem materiału, wymagany jest link do źródła.

Stosowanie równań jest szeroko rozpowszechnione w naszym życiu. Wykorzystywane są w wielu obliczeniach, budowie konstrukcji, a nawet sporcie. Równania były używane przez człowieka od czasów starożytnych i od tego czasu ich użycie tylko wzrosło. W matematyce są zadania, w których konieczne jest poszukiwanie rozwiązań równań liniowych i kwadratowych w postaci ogólnej lub poszukiwanie liczby pierwiastków, które równanie ma w zależności od wartości parametru. Wszystkie te zadania z parametrami.

Rozważ następujące równania jako ilustrujący przykład:

\[y = kx,\] gdzie \ - zmienne, \ - parametr;

\[y = kx + b,\] gdzie \ - zmienne, \ - parametr;

\[ax^2 + bx + c = 0,\] gdzie \ jest zmienną, \[a, b, c\] jest parametrem.

Rozwiązanie równania z parametrem oznacza z reguły rozwiązanie nieskończonego zestawu równań.

Stosując się jednak do pewnego algorytmu, można łatwo rozwiązać następujące równania:

1. Określ „kontrolne” wartości parametru.

2. Rozwiąż oryginalne równanie dla [\x\] za pomocą wartości parametrów określonych w pierwszym akapicie.

3. Rozwiąż oryginalne równanie dla [\x\] z wartościami parametrów, które różnią się od wybranych w pierwszym akapicie.

Załóżmy, że dane jest następujące równanie:

\[\mid 6 - x \mid = a.\]

Po przeanalizowaniu wstępnych danych jest jasne, że \[\ge 0.\]

Zgodnie z zasadą modułu \ wyrażamy \

Odpowiedź: \ gdzie \

Gdzie mogę rozwiązać równanie z parametrem online?

Możesz rozwiązać równanie na naszej stronie https: // site. Darmowy solver online pozwoli Ci rozwiązać równanie online o dowolnej złożoności w ciągu kilku sekund. Wszystko, co musisz zrobić, to po prostu wprowadzić swoje dane do solvera. Możesz również obejrzeć instrukcję wideo i dowiedzieć się, jak rozwiązać równanie na naszej stronie internetowej. A jeśli masz jakieś pytania, możesz je zadać w naszej grupie Vkontakte http://vk.com/pocketteacher. Dołącz do naszego grona, zawsze chętnie Ci pomożemy.

Uwaga . W powyższym przykładzie obliczenie wszystkich determinant zakończyło się przedstawieniem w postaci iloczynu czynników, z których jeden (13) został zredukowany podczas dzielenia. Ta sytuacja jest bardzo ogólna. Dlatego nie spiesz się z mnożeniem współczynników, chociaż najczęściej nie anulują.

Zadanie 4.4. Rozwiąż układy równań za pomocą reguły Cramera:

Rozwiązanie powyższych problemów pokazuje, że wzory Cramera są jednolitą i wygodną metodą znajdowania rozwiązań układów równań liniowych.

Notatka . Stosowanie wzorów Cramera jest znacznie uproszczone, jeśli tylko jedna z niewiadomych ma zostać znaleziona: w tym przypadku należy policzyć tylko dwie determinanty.

2.4.4. Układy równań z parametrami

Powyżej wszędzie rozważano układy liniowych równań algebraicznych ze stałymi współczynnikami dla niewiadomych i prawych stron równań. W problemach praktycznych bardzo często te współczynniki i wartości prawych stron są znane niedokładnie. Dlatego konieczne jest przeanalizowanie wpływu takich parametrów na rozwiązanie układów.

Przykład 4.5. Zbadaj zależność rozwiązania układu równań

3x + 8y = a5x + 9y = b

z parametrów a i b .

Tutaj tylko prawe strony równań zależą od parametrów. O ile

aby znaleźć rozwiązanie, możesz skorzystać ze wzorów Cramera. Mamy:

y (a , b )

x (a , b )

Zatem każda para parametrów aib odpowiada jedynej parze liczb x i y, która spełnia dany układ równań. Oznacza to, że rozwiązaniem układu równań jest para uporządkowana i dwie funkcje dwóch zmiennych (parametry aib). Obie funkcje są zdefiniowane dla dowolnych wartości tych parametrów i zależą liniowo od zmiennych niezależnych a i b . Ponadto x jest monotonicznie rosnący

i zbadać zależność ich rozwiązania od parametrów a i b . Rekomendacje. Wykreśl otrzymane rozwiązania x (a , b ) i y (a , b )

jako funkcje zmiennych parametrów a i b . Wyjaśnij, dlaczego we wszystkich problemach rozwiązania zależą liniowo od parametrów aib .

Przykład 4.6. Zbadaj zależność rozwiązania układu równań

Wyznacznik ten nie jest równy zero tylko wtedy, gdy a − 5. Dlatego ze wzorów Cramera można używać tylko wtedy, gdy a − 5. W tym przypadku:

Rozważmy oddzielnie przypadek a = − 5 . Wtedy oryginalny system to:

− 2 x −10 r = 5 x +5 r = b

− 5 − c x = c , y = 2

Oczywiście istnieje dowolność w wyborze wartości którejkolwiek z niewiadomych, a rozwiązanie można również zapisać w postaci:

x = − 5 2 − 5 c , y = c

Zatem zależność od parametru współczynników dla niewiadomych pierwotnego układu może generować brak rozwiązania lub obecność nieskończonego zbioru rozwiązań. Odkryty fakt jest uogólnieniem znanego wcześniej dla jednego równania ax = b oraz dla układów dwóch równań liniowych z dwiema niewiadomymi.

Uwaga 1. Wprowadzenie stałej c do rozwiązania układu równań przypomina dowolność wyboru stałej całkowania.

Uwaga 2. Rozważany przykład pokazuje, że jak dla pojedynczego równania, dla liniowych układów algebraicznych o dużej liczbie równań i niewiadomych możliwe są tylko trzy różne przypadki: jedno rozwiązanie, brak rozwiązania lub nieskończenie wiele rozwiązań.

Problem 4.6. Poznaj rozwiązania układu równań:

Problem 4.7. Wymyśl własny system dwóch równań algebraicznych z dwiema niewiadomymi i dwoma parametrami i zbadaj go w zależności od wartości parametrów.

Pytania do samokontroli

1) Jaki jest drobny element wyznacznika?

2) Jaka jest różnica między dopełnieniem algebraicznym a molowym elementu wyznacznika?

3) Co to jest macierz sprzężona?

4) Jak znaleźć powiązaną macierz dla danej macierzy?

5) Jaka jest kolejność powiązanej macierzy?

6) Kiedy nie istnieje macierz odwrotna?

7) Jaka macierz nazywa się niezdegenerowaną?

8) W jakich warunkach można stosować formuły Cramera?

9) Jakie jest rozwiązanie układu liniowych równań algebraicznych?

10) Jakie wyznaczniki znajdują się we wzorach Cramera?

11) Kiedy determinanty zależą od parametrów?

12) Czy iloczynem dołączonej i oryginalnej macierzy może być macierz skalarna?

13) Jak permutacja czynników wpływa na wynik mnożenia macierzy skojarzonych i pierwotnych?

14) Jakie są formuły Cramera?

15) W jakich warunkach można znaleźć rozwiązanie układu liniowych równań algebraicznych za pomocą reguły (wzory) Cramera?

Rozwiążmy układ równań z parametrem (A. Larin, opcja 98)

Znajdź wszystkie wartości parametru , dla każdego z których system

ma dokładnie jedno rozwiązanie.

Przyjrzyjmy się bliżej systemowi. W pierwszym równaniu układu po lewej stronie jest , a po prawej stronie nie zależy od parametru. Oznacza to, że możemy uznać to równanie za równanie funkcji

i możemy wykreślić tę funkcję.

Drugie równanie układu

zależy od parametru, a wybierając pełny kwadrat po lewej stronie równania, otrzymujemy równanie koła.

Dlatego sensowne jest budowanie wykresów każdego równania i sprawdzanie, przy jakiej wartości parametru te wykresy mają jeden punkt przecięcia.

Zacznijmy od pierwszego równania. Najpierw otwórzmy moduły. Aby to zrobić, przyrównujemy każde wyrażenie submodułu do zera, aby znaleźć punkty, w których zmienia się znak.

Pierwsze wyrażenie submodułu zmienia znak na , drugie na .

Umieśćmy te punkty na linii współrzędnych i znajdźmy znaki każdego wyrażenia submodułu na każdym przedziale:

Zauważ, że dla i równanie nie ma sensu, więc wycinamy te punkty.

Teraz rozszerzmy moduły na każdym interwale. (Przypomnijmy: jeśli wyrażenie podmodułu jest większe lub równe zero, to rozszerzamy moduł o ten sam znak, a jeśli jest mniejsze od zera, to o przeciwny znak.)

Oba wyrażenia submodułów są ujemne, dlatego oba moduły są rozwinięte o przeciwny znak:

Oznacza to, że pierwotna funkcja ma postać

Na tym przedziale pierwsze wyrażenie submodułu jest ujemne, a drugie dodatnie, dlatego otrzymujemy:

- funkcja nie istnieje w tym przedziale.

3.title="(!JĘZYK:x>2">!}

Na tym przedziale oba wyrażenia submodułów są dodatnie, oba moduły rozszerzamy o ten sam znak. Otrzymujemy:

Oznacza to, że z tytułem="(!LANG:x>2"> исходная функция имеет вид !}

Więc mamy wykres funkcji

Spójrzmy teraz na drugie równanie:

Wybieramy pełny kwadrat po lewej stronie równania, w tym celu dodajemy liczbę 4 po obu stronach równania:

Dla określonej wartości parametru wykres tego równania jest okręgiem wyśrodkowanym w punkcie o współrzędnych , którego promień jest równy 5. Dla różnych wartości mamy ciąg okręgów:

Przesuniemy okrąg od dołu do góry, aż dotknie lewej strony wykresu pierwszej funkcji. Na rysunku ten okrąg jest czerwony. Środek tego okręgu to punkt , jego współrzędne to (-2;-3). Dalej, poruszając się w górę, okrąg ma jeden punkt przecięcia z lewą stroną wykresu funkcji, czyli system ma unikalne rozwiązanie.

Kontynuujemy przesuwanie koła w górę, aż dotknie prawej strony wykresu pierwszej funkcji. Stanie się tak, gdy środek okręgu znajdzie się w punkcie o współrzędnych (-2; 0) - na rysunku ten okrąg jest niebieski.

Idąc dalej w górę, okrąg będzie przecinał zarówno lewą, jak i prawą część wykresu pierwszej funkcji, czyli okrąg będzie miał dwa punkty przecięcia z wykresem pierwszej funkcji, a układ będzie miał dwa rozwiązania. Ta sytuacja trwa do momentu, gdy środek okręgu znajdzie się w punkcie o współrzędnych (-2; 5) - ten okrąg jest zielony. W tym momencie okrąg dotyka lewej strony wykresu i przecina prawą stronę. Oznacza to, że system ma jedno rozwiązanie.

System posiada więc unikalne rozwiązanie dla (-3;0]}